Description
佩奇和乔治在爬♂树。
给定 n 个节点的树 T(V,E),第 i 个节点的颜色为 wi,保证有 1≤wi≤n。
对于 1≤i≤n,分别输出有多少对点对 (u,v),满足 u<v,且恰好经过所有颜色为 i 的节点,对于节点颜色不为 i 的其他节点,经过或不经过均可。
树上路径 (u,v) 定义为序列 {f},满足 f1=u,f∣f∣=v,且 ∀1≤i<∣f∣,T 中均存在边 (fi,fi+1),且 {f} 中无重复元素,能够证明对于任意点对 (u,v),其树上路径唯一。
第一行 1 个正整数,表示 n 。
第二行 n 个正整数,第 i 个正整数表示 wi。
之后 n−1 行,每行 2 个正整数 u,v,表示 T 中存在边 (u,v)。
共 n 行,每行 1 个正整数,第 i 行输出包含所有颜色为 i 的节点的路径个数。
4
1 2 2 3
1 2
2 3
3 4
3
4
3
6
10
9 7 4 2 3 4 4 5 8 5
2 1
3 2
4 2
5 2
6 4
7 4
8 1
9 4
10 4
45
35
9
0
1
45
34
9
17
45
Hint
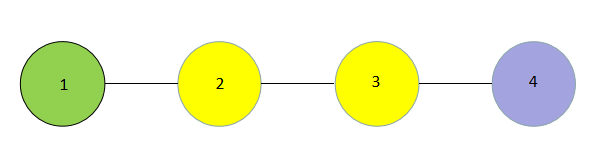
对于第一组样例而言。
对于颜色 1,点对 (1,2),(1,3),(1,4) 满足条件。
对于颜色 2,点对 (1,3),(1,4),(2,3),(2,4) 满足条件。
对于颜色 3,点对 (1,4),(2,4),(3,4) 满足条件。
对于颜色 4,由于图中没有颜色为 4 的节点,所以所有点对均满足条件。
数据范围
对于 40% 的数据,n≤102。
对于 60% 的数据,n≤103。
对于 100% 的数据,n≤106。


 京公网安备 11011102002149号
京公网安备 11011102002149号