#P5564. [Celeste-B] Say Goodbye
[Celeste-B] Say Goodbye
Description
Madeline 将收集到的草莓分给了朋友们
火红色的草莓和金黄色的草莓交错在一起,很受朋友们喜爱
朋友们为了感谢 Madeline ,一起收集了许多五颜六色的珠子,打算串成一条花花绿绿的项链送给 Madeline
经过朋友们的精心准备,现在桌子上摆着个珠子,这些珠子一共有种颜色。具体来说,第种颜色的珠子有个
看着桌子上晶莹剔透的珠子,现在朋友们却犯难了,因为他们不知道怎样将它们串在一起才最美丽
朋友们向你发出了请求,需要你帮忙求出本质不同的方案总数
朋友们分不清这些珠子的顺序,因此两个珠子不同仅当它们的颜色不同
这条项链必须是完整的,因此所有珠子构成了一个连通块
这条项链还不能太杂乱,因此所有珠子必须构成一棵基环树
在多次询问 Madeline 的朋友们之后,你发现这棵基环树的两个子树不同仅当它们对应点的颜色不同或者这两棵子树不同构。对于不同的子树是有先后顺序之分的
举例来说,下面的几种部分串法是互不相同的
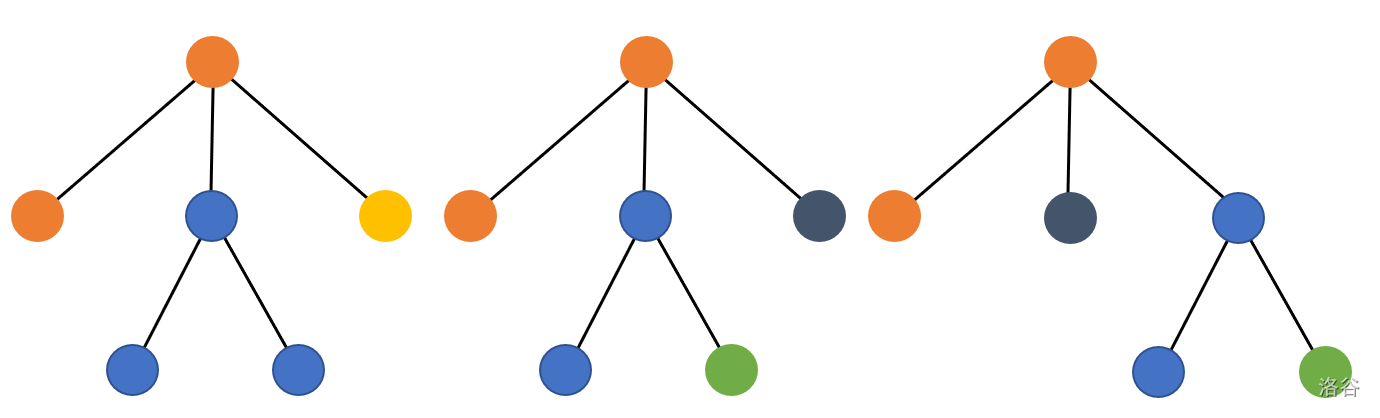
朋友们的时间很紧迫,因此如果两种项链能够通过旋转基环得到同样的结果,那么这两种项链本质上是相同的
Input Format
第一行两个整数 ,分别表示珠子的总数以及颜色种数
接下来一行 个整数 ,表示每种颜色的珠子个数
Output Format
输出一个整数,表示方案数模 的余数
3 3
1 1 1
8
4 2
1 3
15
Hint
基环树:一个有个点条边的联通图,没有自环。容易看出这样的图是一个环上连出了一些树
基环:基环树中的环
对于 的数据,
对于另 的数据,
对于前 的数据,
对于另 的数据,
对于前 的数据,
对于 的数据,$a_i > 0 , \sum a_i = n , n \leq 2 \times 10^5 , k \leq n$
第二个样例解释:
有如下种情况:


 京公网安备 11011102002149号
京公网安备 11011102002149号