#P5517. [MtOI2019] 幻想乡数学竞赛
[MtOI2019] 幻想乡数学竞赛
Description
存在一个数列 。
已知 $a_0=-3,a_1=-6,a_2=-12,a_n=3a_{n-1}+a_{n-2}-3a_{n-3}+3^n$。
-
现在给你一个非负整数 ,令 ,请你求出 。
-
注:若 ,请输出 。
为了更充分地考验你的水平,荷取设置了 组询问。
- 为了在某种程度上减少你的输入和输出量,我们采用以下的代码来生成询问:
namespace Mker
{
// Powered By Kawashiro_Nitori
// Made In Gensokyo, Nihon
#include<climits>
#define ull unsigned long long
#define uint unsigned int
ull sd;int op;
inline void init() {scanf("%llu %d", &sd, &op);}
inline ull ull_rand()
{
sd ^= sd << 43;
sd ^= sd >> 29;
sd ^= sd << 34;
return sd;
}
inline ull rand()
{
if (op == 0) return ull_rand() % USHRT_MAX + 1;
if (op == 1) return ull_rand() % UINT_MAX + 1;
if (op == 2) return ull_rand();
}
}
在调用 Mker::init() 函数之后,你第 次调用 Mker::rand() 函数时返回的便是第 次询问的 。
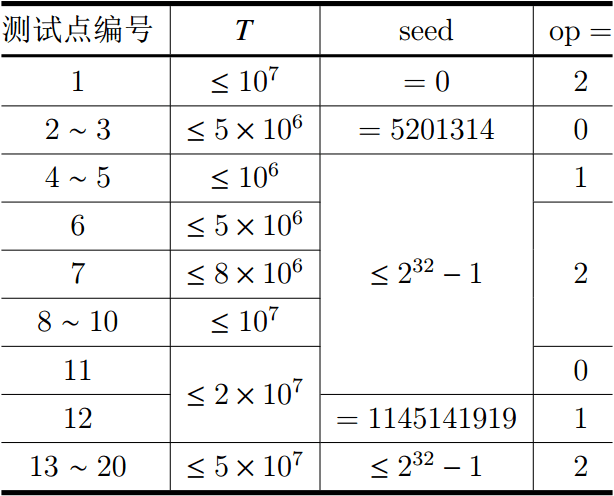
在这里给出 的限制:
-
如果 ,满足 。
-
如果 ,满足 。
-
如果 ,满足 。
为了减少你的输出量,你只需要输出所有询问答案的异或和。
Input Format
第一行三个整数,输入 , 和 。
Output Format
第一行一个整数,输出 组询问的答案的异或和。
142857 1145141919 0
562611141
142857 1145141919 1
894946216
142857 1145141919 2
771134436
Hint
子任务
题目来源
迷途之家 2019 联赛(MtOI2019) T4
出题人:disangan233
验题人:suwakow

 京公网安备 11011102002149号
京公网安备 11011102002149号