#P5441. 【XR-2】伤痕
【XR-2】伤痕
Description
X 国经历了一场前所未有的大地震,人们伤痕累累,整个国家破碎不堪。
为了帮助人们痊愈,也为了让 X 国能够生存下去,X 国国王决定重建 X 国。
国王决定先建造 座城市,由于国王喜欢奇数,所以 为奇数。
城市建造完后,需要给每两座城市之间都修建一条道路,即一共需要修建 条道路。
不过,修建双向道路的成本太高了,建造完 座城市后剩下的经费最多只够修建 条双向道路,而其余的道路只能修建成单向的。好在方向并不会影响修建单向道路所需的费用,因此所有单向道路的方向可以任意决定。
另外,等到重建完成后,国王决定将 座城市钦定为 X 国的核心城市。为促进 X 国的发展,这 座核心城市中的任意两座城市,必须能够在不经过非核心城市的情况下相互到达。
国王希望,你能够给他一种道路修建方案,使重建完成后选择 座核心城市的方案数最大化。
Input Format
一行一个正整数 ,保证 为奇数,表示有 座城市。
Output Format
第一行包含一个整数,表示最大的选择 座核心城市的方案数。
接下来的 行每行 个正整数描述一个邻接矩阵,表示你的道路修建方案。
具体来说,第 行的第 个数为 表示第 座城市可以通过一条道路到达第 座城市,为 表示第 座城市无法通过一条道路到达第 座城市。我们分为 种情况详细说明:
- 之前的道路为一条 到 的单向道路,则邻接矩阵的第 行第 个数为 ,第 行第 个数为 。
- 之间的道路为一条双向道路,则邻接矩阵的第 行第 个数和第 行第 个数均为 ,你需要保证最多修建 条双向道路。
- ,则第 行第 个数(第 行第 个数)为 。
3
0
0 1 1
0 0 1
0 1 0
5
5
0 1 0 1 1
0 0 1 1 0
1 0 0 0 1
1 0 1 0 1
1 1 0 0 0
Hint
【样例 说明】
由于一共只有 个点,所以选择 座核心城市的方案数一定为 ,那么只需要保证修建方案满足条件即可。
【样例 说明】
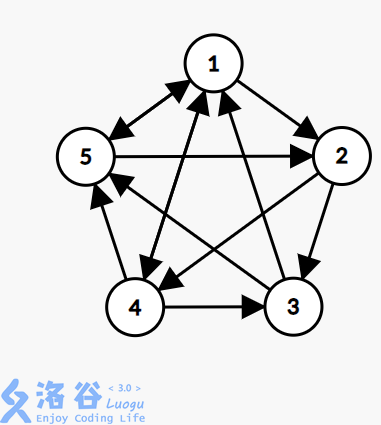
显然,在 个点中任意选 个点,都满足核心城市的条件,因此方案数最大为 。
【数据规模与约定】
本题一共有 个测试点,每个测试点 分。对于第 个测试点,。
对于每个测试点,有五种可能的结果:
- 输出格式错误,包括:没有输出最大方案数、没有输出邻接矩阵、输出了多余的信息等。你将无法得到该测试点的任何分数,同时我们无法确定 Special Judge 的返回结果。
- 没有正确计算最大方案数,即使构造的道路修建方案是正确的。你将得到该测试点 的分数(即 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is wrong.”
- 正确计算了最大方案数,但是构造的道路修建方案不满足条件,包括:邻接矩阵中有不为 或 的数、有自环、有两座城市中没有道路、有多于 条双向道路等。你将得到该测试点 的分数(即 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is correct, but your plan breaks the rules.”
- 正确计算了最大方案数,构造的道路修建方案满足条件但没有将选择 座核心城市的方案数最大化。你将得到该测试点 的分数(即 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is correct, but your plan is wrong.”
- 正确计算了最大方案数,同时正确构造了道路修建方案。你将得到该测试点 的分数(即 分),Special Judge 将会返回 AC 的结果,同时输出 “The answer is correct.”

 京公网安备 11011102002149号
京公网安备 11011102002149号