Description

为了防止神J用篮球造出一个指针把自己指出去，神树大人钦定神J用篮球造一个矩阵。

这个矩阵无限大，行列从0开始标号，且$a[i][j]=i\ xor\ j$

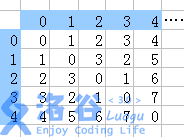
现在，对于一个左上角为$(lx,ly)$，右下角为$(rx,ry)$的子矩阵，$K(K\leq 10^9)$次随机从里面取$W\times H$的矩阵，问取出的矩阵完全一样的概率，对$10^9+7$取模。

Input Format

第一行一个数$Q$表示$Q$组询问

之后$Q$行每行7个数$lx,rx,ly,ry,W,H,K$

Output Format

输出答案对$10^9+7$取模。保证答案存在。

5
54 63 5 59 5 27 2
33 42 1 29 9 23 2
54 55 56 57 2 1 3
40 64 17 40 19 9 1
54 65 35 50 3 10 3

626436786
71428572
250000002
1
154489797

3
1 2 1 2 1 1 2
3 100 39 100 1 1 2
48395 309846 34098 234095 1 1 2

500000004
779746001
262016540

Hint

对于1 2 1 2 1 1 2这组询问

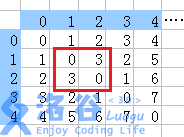
可以取的矩阵有：0,3，各出现两次。

有如下情况：

第一次取到 3，第二次取到 0，一共4种方法

第一次取到 3，第二次取到 3，一共4种方法

第一次取到 0，第二次取到 0，一共4种方法

第一次取到 0，第二次取到 3，一共4种方法

一共16种方法，符合条件的有4+4=8种

所以答案为 8/16=500000004(mod 10^9+7)

##数据范围

对于所有的数据，$0\leq lx\leq rx\leq 10^9,0\leq ly\leq ry\leq 10^9,W\leq rx-lx+1,H\leq ry-ly+1,1\leq K\leq 10^9,Q\leq 10^3$

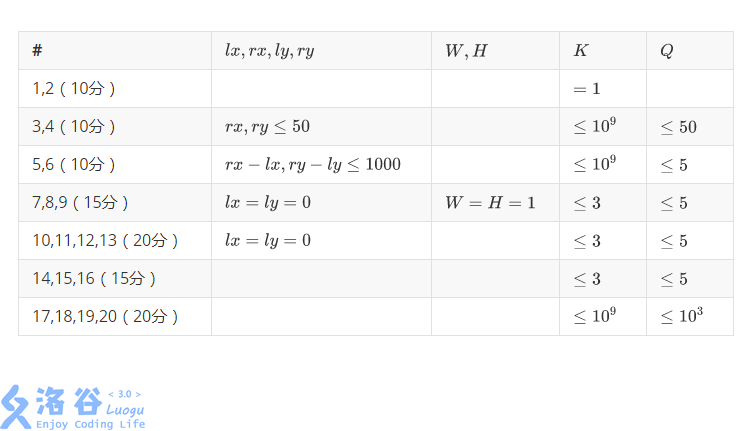
空格为无特殊限制