Description

给你一个有 $n$ 个点和 $m$ 条边的仙人掌图，和 $q$ 组询问
每次询问两个点 $u,v$，求两点之间的最短路。

保证输入数据没有重边。

Input Format

第一行三个正整数 $n,m,q$，意义如题目描述。
接下来 $m$ 行，每行三个正整数 $u,v,w$，表示 $u,v$ 之间有一条权值为 $w$ 的无向边。
然后 $q$ 行，每行两个正整数 $u,v$，询问 $u$ 到 $v$ 的最短路。

Output Format

$q$ 行，每行一个正整数，对应一次询问的结果。

9 10 2
1 2 1
1 4 1
3 4 1
2 3 1
3 7 1
7 8 2
7 9 2
1 5 3
1 6 4
5 6 1
1 9
5 7

5
6

9 10 3
1 2 1
2 3 1
2 4 4
3 4 2
4 5 1
5 6 1
6 7 2
7 8 2
8 9 4
5 9 2
1 9
5 8
3 4

7
5
2

Hint

样例1解释：
样例1中的仙人掌是这个样子的：

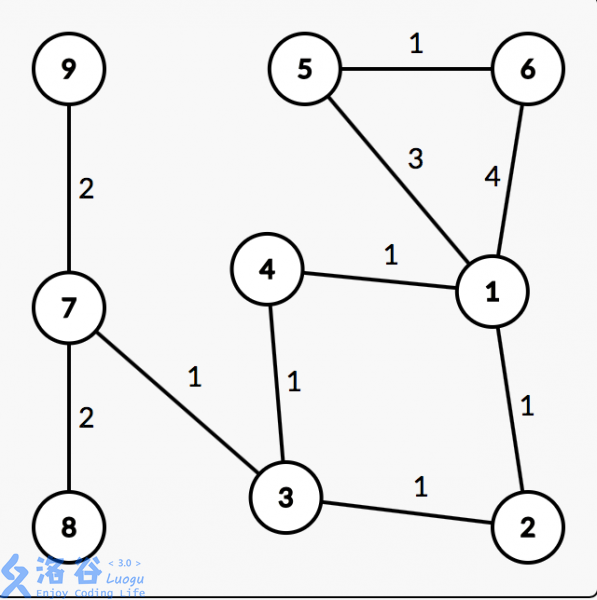
询问有两个，分别是询问 $1\rightarrow 9$ 和 $5\rightarrow 7$ 的最短路
显然答案分别为 $5$ 和 $6$。

数据范围：
$1\le n,q \le 10000$
$1\le m \le 20000$
$1\le w \le 10^5$

保证输入数据没有重边。

请注意时限为 $300\text{ms}$