题目背景

融合了强力的装备,当然要去探索迷宫了

题目描述

然而，在你用一套神装愉快的切瓜切菜时，慧音大小姐对你发动了忘却技能，于是，没有融合"记"印记的你忘记了迷宫的构造。

由于在忘却前你对这个迷宫的构造已经了如指掌，所以你知道这个迷宫的 $n$ 个房间都是互相连通的，并且有 $n$ 条道路连接这些房间(当然，道路从两个方向都可以经过)

即使在不可思议的幻想乡，基本的常识也是存在的，也就是说不会有连接两个相同房间的道路，也不会有两端是同一个房间的道路。

忘记了迷宫的构造后，你无从得知你在哪里，以及前往下一层的通道在哪里.幸运的是，你保存了一份这个迷宫大致的地图，知道了这 $n$ 条道路分别连接哪两个房间以及每条道路的长度。

为了通关，你会从你所在的位置(某个随机的位置)不重复经过道路地走向前往下一层的通道(某个随机的位置)，显然，这种路径可能不止 $1$ 条，那么这时你会随机选取其中一条。

现在，你想知道自己走过的路径的期望长度，为了避免精度误差，只要对 $19260817$ 取模就好了。

输入格式

第一行一个整数 $n$，表示房间以及道路的个数。

下面 $n$ 行每行三个整数 $u,v,w$，表示从房间 $u$ 到房间 $v$ 有一条长度为 $w$ 的道路。

输出格式

一行一个整数，表示期望路径长度。

4
1 4 2
4 2 2 
3 4 2
2 3 2

8426611

提示

样例解释:

迷宫的结构如下:

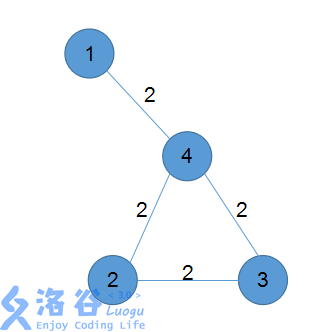
起始点和结束点都是随机的，用二元组$(x,y)$表示

以几个有代表性的二元组为例:

$(1,1)$，只有一条长度为$0$的路径

$(1,2)$，有两条路径$1-4-2,1-4-3-2$，期望路径长度为 $\frac{4+6}{2}=5$
$(3,3)$，有两条路径$3-2-4,3$，期望路径长度为 $\frac{6+0}{2}=3$

不难算出，将所有可能的二元组的期望路径长度加在一起为$57$，所以答案为 $\frac{57}{16}$ ,在模意义下等于 $8426611$。

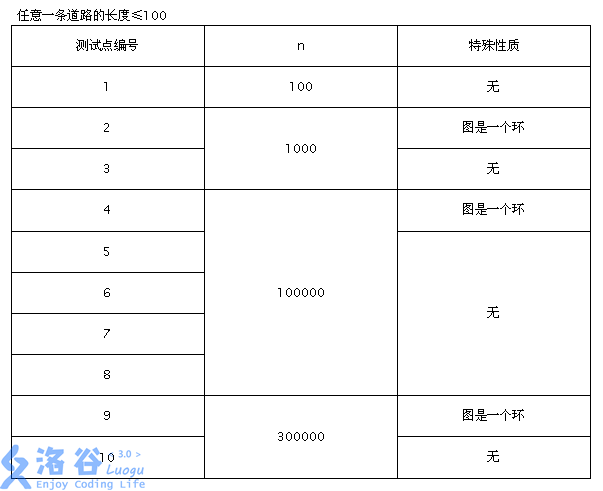
数据范围: