#P5100. [JOI 2017 Final] 足球 / Soccer
[JOI 2017 Final] 足球 / Soccer
Description
题目译自 JOI 2017 Final T4「サッカー / Soccer」
「假定球滚动时可以穿过其他球员」这句是在未修改数据的前提下,为了严谨我补上的,原题没有提这一点。如果撞到其他球员就停下的话似乎做法不同?
你是 JOI 联赛中一所声名卓著的足球俱乐部的经理。
俱乐部有 名球员,编号为 。球员们每天都刻苦地进行训练,剑指联赛冠军。足球场可视为一个底为 米,高 米的长方形,底平行于东西方向,高平行于南北方向。如果某个点向北走 米,再向西走 米恰好到达球场的西北角,这个点可用坐标 来表示。
练习结束后,你要回收练习用的足球。开始回收时,所有球员都在足球场上,球员 位于 ,球在球员 脚下。你正和球员 一起站在 ,并准备回收球。球员们把球传到 时,你才会回收球。
你可以指挥球员,但某些操作会提升球员的疲劳度。一个球员不能同时进行多项操作。
你可以指挥控球的球员进行如下操作:
- 踢球。在东西南北四个方向中任选一个,并指定一个正整数 ,该球员将球朝指定方向踢出恰好 米。假定球滚动时可以穿过其他球员。该球员不会移动,且自动停止控球,疲劳度上升 。
- 运球。在东西南北四个方向中任选一个,该球员带球,朝指定方向移动 米。该球员仍然控球,疲劳度上升 。
- 停止控球。该球员的疲劳度不改变。
你可以指挥没有控球的球员进行如下操作:
- 移动。在东西南北四个方向中任选一个,该球员朝指定方向移动 米,疲劳度上升 。
- 控球。如果该球员所在的位置恰好有球,且没有其他球员控球,该球员才能控球。该球员的疲劳度不改变。
球员和球有可能跑出场外,一个位置上可能有多个球员。
一天的训练结束后,球员们非常疲惫。你想知道在回收球的过程中,所有球员上升的疲劳度之和的最小值。
Input Format
第一行有两个整数 ,用空格分隔。
第二行有三个整数 ,用空格分隔。
第三行有一个整数 。
在接下来的 行中,第 行 有两个整数 ,用空格分隔。
输入的所有数的含义见题目描述。
Output Format
一行,一个整数,表示在回收球的过程中,所有球员上升的疲劳度之和的最小值。
6 5
1 3 6
3
1 1
0 4
6 5
26
3 3
0 50 10
2
0 0
3 3
60
4 3
0 15 10
2
0 0
4 3
45
4 6
0 5 1000
6
3 1
4 6
3 0
3 0
4 0
0 4
2020
Hint
样例解释 1
在这组样例中,球场、球员、球处于如图所示的状态。图中,黑框空心圆圈表示球员,实心圆表示球,你在 。
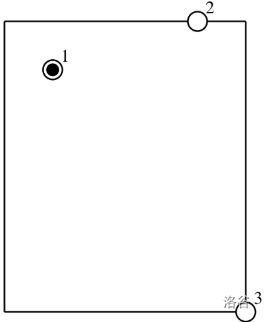
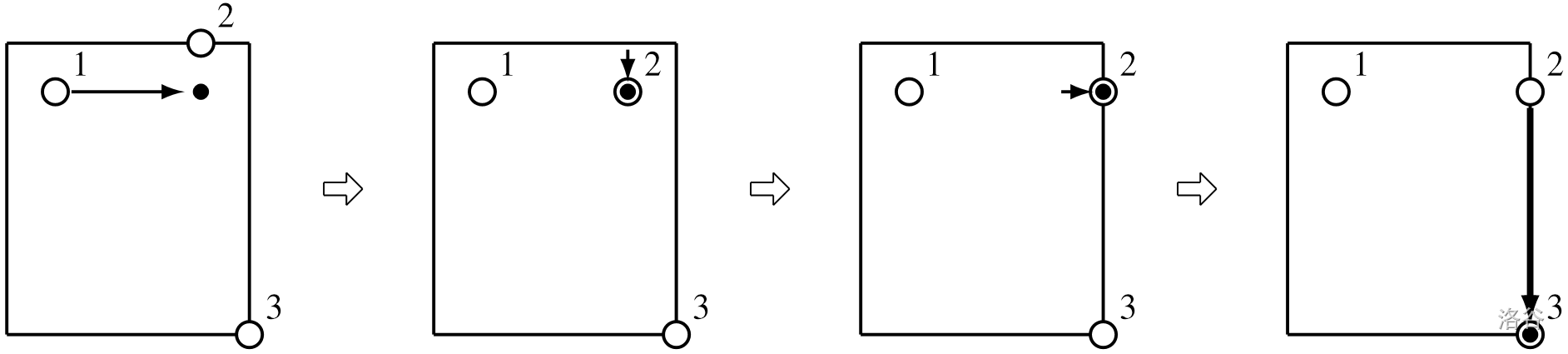
最优解如下:
- 球员 把球向东踢出 米。疲劳度上升了 ,球移动到 。
- 球员 向南移动 米。疲劳度又上升了 。
- 球员 开始控球。
- 球员 向东运球 米。疲劳度又上升了 。
- 球员 把球向南踢出 米,疲劳度上升了 ,球移动到 。
此时,疲劳度之和为 。没有更好的方案。
样例解释 2
在最优解中,不需要踢球。
样例解释 4
注意这组样例中有多个球员在同一位置的情况。
数据范围与提示
对于 的数据,。
对于另外 的数据,。
对于所有数据,$1\leqslant H,W\leqslant 500, 0\leqslant A, B, C\leqslant 10^9, 2\leqslant N\leqslant 10^5, 0\leqslant S_i\leqslant H, 0\leqslant T_i\leqslant W(1\leqslant i\leqslant N), (S_1, T_1)\neq(S_N, T_N)$。

 京公网安备 11011102002149号
京公网安备 11011102002149号