题目背景

本题译自 eJOI2018 Problem E「Prime Tree」

题目描述

本题为提交答案，输入文件在附件中。

设有一棵有 $n$ 个结点的树，其结点编号为 $1$ 到 $n$ 。
对于其中的任意一条边 $(u, v)$ ，如果存在一个正整数 $d>1$ 满足 $d \mid u, d\mid v$ ，我们称它为一条坏的边。
下图中的树有三条坏的边—— $(6, 4)$（都被 $2$ 整除）， $(2, 6)$（都被 $2$ 整除）， $(3, 6)$（都被 $3$ 整除）。

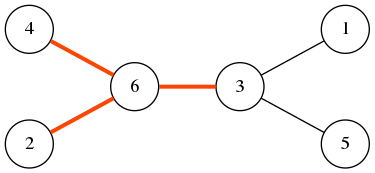
你的任务是将结点重新编号，使得图中坏的边的数量尽量少。
对于上图中的树，按照下图中的方式将结点重新编号，会只剩一条坏的边 $(3, 6)$ 。

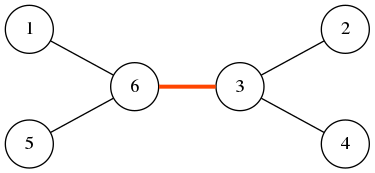
重新编号后，坏的边越少，你的得分越高。

这是一道提交答案题。你应当下载输出文件，然后在本地运行你的程序，将输出结果上传。当然，在洛谷上你可以直接提交你的程序。

输入格式

每个测试点中有多组测试数据。
第一行，一个整数 $T$，表示测试数据组数。
每组测试数据共 $n$ 行，其中 $n$ 表示树的结点个数。
第一行，一个整数 $n$；
接下来 $n-1$ 行，每行两个整数 $u$ 和 $v\ ( 1 \le u, v \le n)$，表示一条边 $(u,v)$ 。

每个输入文件中，每棵树的结点个数相同。

输出格式

对于每组测试数据，输出一行 $n$ 个整数，表示原先编号为 $1$ 到 $n$ 的结点的新编号。
每个结点的编号必须不同，也就是说同一组测试数据中输出的 $n$ 个整数必须互不相同。

2
6
1 3
3 5
3 6
6 4
6 2
6
1 2
1 3
1 4
1 5
1 6

2 5 3 1 4 6
5 1 2 3 4 6

4 5 1 3 6 2 
5 4 6 1 3 2

提示

计分方式

对于每个测试点，设所有树的总边数为 $M=T \times (n-1)$，你的输出中坏的边数为 $X$，记 $R=\dfrac{X}{M}$ ，你的得分与 $R$ 的关系如下：

$R$	得分	$R$	得分
$0.33 < R \le 0.4$	$1$	$0.01 < R \le 0.05$	$6$
$0.26 < R \le 0.33$	$2$	$0.005 < R \le 0.01$	$7$
$0.19 < R \le 0.26$	$3$	$0.001 < R \le 0.005$	$8$
$0.12 < R \le 0.19$	$4$	$0 < R \le 0.001$	$9$
$0.05 < R \le 0.12$	$5$	$R=0$	$10$

当 $R > 0.4$ 时，不能得分。

对于所有的测试点，保证存在 $X=0$ 的输出。

---

样例解释

注意样例中给出了两种合法的输出，为了方便，下称输出 1 和 输出 2。

第一组测试数据已经在题目描述中讨论过。输出 1 中有一条坏的边 $(3, 6)$，输出 2 中没有坏的边。
第二组测试数据中，输出 1 和输出 2 都没有出现坏的边。

样例中，$M=2 \times 5=10$。

对于输出 1，$X=1, R=\dfrac{1}{10}=0.1$，该输出将得到 $5$ 分。

对于输出 2，$X=0, R=\dfrac{0}{10}=0$，该输出将得到 $10$ 分。

---

数据范围和限制

数据限制

• 对于测试点 1 （输入 01），$T=3, n=7$，三棵树分别如下所示：

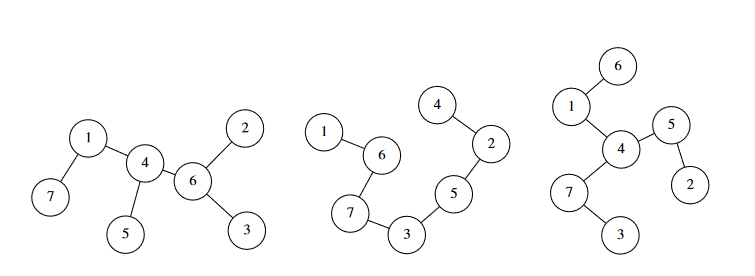
• 对于测试点 4 至 8 （输入 04 至 08），输入数据有特殊性质（如叶子结点较多，是二叉树等），且这些具有特殊性质的树在各个测试点中输入数据均匀分布。

• 对于其他测试点，数据为随机生成。

数据范围

测试点编号	1	2	3	4	5	6	7	8	9	10
文件名	01	02	03	04	05	06	07	08	09	10
$T$	$3$	$100$		$500$	$200$	$50$	$10$	$5$	$2$	$1$
$n$	$7$	$10$	$30$	$100$	$500$	$2000$	$10000$	$20000$	$50000$	$100000$