题目背景

本题译自 eJOI2018 Problem D「Chemical table」

题目描述

Innopolis 大学的教授正努力研究元素周期表。他们知道，有 $n \times m$ 种元素，形成了一个 $n$ 行 $m$ 列的矩阵。

研究表明，如果元素周期表上有一个元素 A，且元素 B 与它在同一列（A 与 B 不能在同一周期），元素 C 在同一周期（A 与 C 不能在同一列），那么，科学家就可以用这三种元素通过核聚变合成第四种元素 D 的样品，D 与 B 在同一周期，与 C 在同一列。
简而言之，如果有在元素周期表中位置为 $(r_1, c_1),\ (r_1, c_2),\ (r_2, c_1)$ （其中 $r_1 \neq r_2, c_1 \neq c_2$）的三种元素的样品，就可以生成位置为 $(r_2, c_2)$ 的样品。如图所示：

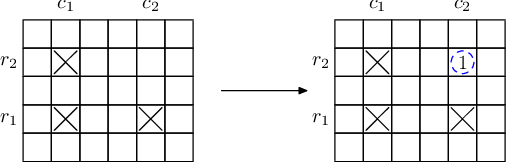
注意：在核聚变中被使用的样品并不会消失，它们可以参与之后的反应；反应得到的样品也可以参与反应。

他们已经获得了 $q$ 种元素的样品。为了集齐所有元素的样品，他们会购买一些样品，然后利用核聚变制造出剩下元素的样品。
请求出他们至少需要购买的元素样品的数量。

输入格式

第一行， $3$ 个整数 $n, m, q \ (1 \le n, m \le 2 \times 10^5, 0 \le q \le \min \{n \times m, 2 \times 10^5\})$ 。
之后的 $q$ 行，每行 $2$ 个整数 $r_i, c_i \ (1 \le r_i \le n, 1 \le c_i \le m)$ 。保证给定的元素互不相同。

输出格式

输出一个整数，表示至少需要购买的元素样品的数量。

2 2 3
1 2
2 2
2 1

0

1 5 3
1 3
1 1
1 5

2

4 3 6
1 2
1 3
2 2
2 3
3 1
3 3

1

提示

样例解释

说明

每个样例解释中有两个矩阵。
第一个表示初始状况（其中，打叉的是原本就有样品的元素）。
第二个表示最终集齐样品时的状况（其中，蓝圈代表核聚变得到的样品，蓝圈中的数字表示得到样品的顺序，红圈表示购买的样品）。

样例解释 1

通过给定的三种元素，可以得到第四种元素的样品。

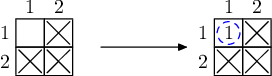
样例解释 2

由于给定的元素只有一行，无法使用核聚变，只能购买剩余的两种元素的样品。

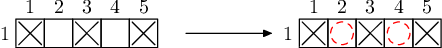
样例解释 3

集齐所有元素的方法不唯一，以下是一种方法。其中，元素 $(4, 2)$ 只有在购买元素 $(4, 1)$ 的样品，和反应得到元素 $(1, 1)$的样品后才能得到。

---

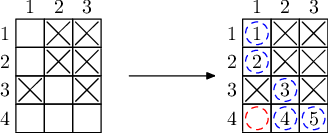
子任务

注意：当且仅当你通过了一个子任务下的所有测试点，你将获得此子任务的分数。

子任务编号	分数	$n$	$m$	$q$
$1$	$10$	$n=2$	$m=2$	$0 \le q \le 4$
$2$	$17$	$1 \le n \le 2$	$1 \le m \le 20$	$0 \le q \le 20$
$3$	$8$	$1 \le n \le 20$		$q=0$
$4$	$20$			$0 \le q \le 400$
$5$	$30$	$1 \le n \le 1 \times 10^4$	$1 \le m \le 1 \times 10^4$	$1 \le q \le 1 \times 10^5$
$6$	$15$	$1 \le n \le 2 \times 10^5$	$1 \le m \le 2 \times 10^5$	$1 \le q \le 2 \times 10^5$