题目描述

有一堆管道，还有一个蜘蛛$\text{Willy}$，如下图所示。所有管道的是上端开口，下端封底，直径都是$1cm$，连接两个管道的连接容量无限，但体积可以忽略不计。

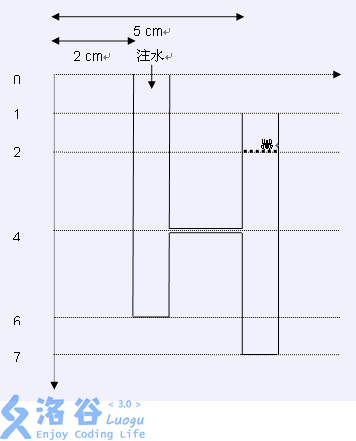
在第一个管道上方有一个水源，从中有水不断往下流，速度为每秒$0.25cm^3$。由于管道横截面积为$0.25cm^3$，所以单给一个管道注水时水面每秒上升$1cm$。根据物理知识，在前$2$秒中，水注如左边的管道底部，第$[3,5]$秒时注入右边的管道，第$[6,9]$秒同时注入两个管道（虽然流量不变，但是由于同时给两个管道注水，因此水面上升的速度仅为每秒$0.5cm$），接触到蜘蛛。 给出管道和管道之间连接的位置，以及蜘蛛$\text{Willy}$的位置，求水面接触到$\text{Willy}$的时间。假设蜘蛛的实际位置比给出的略高一点，因此如果蜘蛛在左边管道的$n=4$的位置，答案应该是$5$秒。因为前两秒后水面虽然看起来接触到了$\text{Willy}$，但实际上比$\text{Willy}$略低一点。

输入格式

所有位置都用有序数对$(x, y)$表示，其中y坐标从上到下逐渐增大；$x$坐标从左到右逐渐增大，因此左上角的坐标为$(0,0)$，其他所有坐标值为$0$到$100$之间的整数。输入第一行为一个整数$p(1<=p<=20)$，表示管道的数目；以下$p$行，每行用$x, y, h$三个整数描述一根管道。$(x,y)$为管道左上角坐标；$h$为管道高度$(1<=h<=20)$。以下一行为一个整数$L(0<=L<=50)$，为连接的个数。

以下$L$行每行用三个整数$x, y, d$描述一个连接，$(x,y)$为左端点的坐标，$d$为连接的长度$(1<=d<=20)$。最后一行为两个整数$a,b$，表示$\text{Willy}$在管道$a$的$y$坐标为$b$的位置。管道按照在文件中出现的顺序编号为$1,2,3…p$

以下为一些假设： 水源总是在第一根管道的正上方, 连接不会穿越管道,任意两个连接的$y$坐标都不相同,任意两个管道的左上角的$x$坐标都不相同,任意连接的两个端点都在管道上（不会出现悬空的情形）

输出格式

仅一个整数，为水面接触到$\text{Willy}$的时间。如果水面无法接触到$\text{Willy}$，输出$-1$。

2
2 0 6
5 1 6
1
3 4 2
2 2

9