Description

This game gives you a tree with $N$ nodes, where the root is $R$. The system will select $M$ nodes $P_1,P_2 \cdots P_M$, and asks Imakf to answer how many ordered pairs of nodes $(u_i, v_i)$ have their lowest common ancestor equal to $P_i$. Imakf is a beginner. Even though he has learned LCA, he still cannot solve it, so he has to ask you for help.

Input Format

The first line contains three integers $N, R, M$.

Then $N - 1$ lines follow, each containing two numbers $a, b$, indicating that there is an edge between $a$ and $b$.

Then $1$ line follows, containing $M$ numbers, indicating $P_i$.

It is guaranteed that the given edges form a tree.

Output Format

Output $M$ lines in total. Each line contains one number. The number on line $i$ indicates how many ordered pairs of nodes $(u_i, v_i)$ have their lowest common ancestor equal to $P_i$.

7 1 3
1 2
1 3
2 4
2 5
3 6
3 7
1 2 4

31
7
1

Hint

The tree of Sample 1 is shown in the figure below:

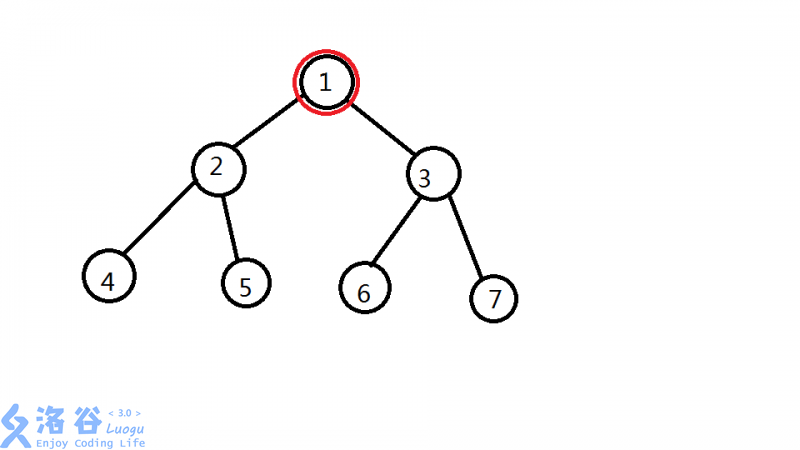
For Query 1 $~(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (1,7) (2,1) (2,3) (2,6) (2,7) (3,1) (3,2) (3,4) (3,5) (4,1) (4,3)$

$(4,6) (4,7) (5,1) (5,3) (5,6) (5,7) (6,1) (6,2) (6,4) (6,5) (7,1) (7,2) (7,4) (7,5)$ there are $31$ ordered pairs in total.

For Query 2 $(2,2) (2,4) (2,5) (4,2) (4,5) (5,2) (5,4)$ there are $7$ ordered pairs in total.

For Query 3 $(4,4)$ there is $1$ ordered pair in total.

Constraints: $1 \le R \le N \leq 10000$, $0 \le M \leq 50000$.

Translated by ChatGPT 5