Description

Time is ticking away second by second, yet Xiao F is still staring at the essay prompt, racking his brain. It looks like he will not finish the essay again.

However, Xiao F has a special trick to pad the word count: keep starting new lines. This is because the essay paper allows $L$ characters per line, and the minimum word count requirement is measured by the number of lines.

That is, as long as he reaches $M$ lines (excluding the title), the requirement is considered met; “reaches” means that the line contains at least one character. Note that due to formatting requirements, the first line of each paragraph has an indentation of two spaces.

Now, he has planned $N$ sentences, and each sentence has its own length $a_i$—including punctuation. We do not consider cases where, for example, a final period would be beyond the last cell and thus avoid wrapping. The connections between these sentences vary in strength: more strongly related sentences are more suitable to be in the same paragraph, while weakly related ones are more suitable to be split into different paragraphs. However, for padding the word count, Xiao F may insert a paragraph break between any two consecutive sentences.

The association between sentences is represented in a special way. We know that when grading, the score is divided into several main parts; for example, the national paper has “Basic,” “Expression,” and “Development,” each with the same total score (e.g., $20$ points). The minimum for each part is $0$ points, meaning that even if a part would go below $0$, it is counted as $0$. Here, our rubric has $K$ parts, each with a full score of $S$. Depending on the aspect, Xiao F uses a $K$-tuple $s_i = (s_{i,1}, s_{i, 2}, \cdots, s_{i, K})$ to describe the relation between sentence $i$ and sentence $i + 1$, where each number is an integer. The $j$-th number $s_{i, j}$ means:

• If it is positive, then splitting sentences $i$ and $i + 1$ will deduct $s_{i, j}$ points from part $j$.
• If it is negative, then not splitting these two sentences will deduct $-s_{i, j}$ points from part $j$.
• If it is $0$, then whether to split has no effect on the score for that part.

Starting from full marks for each part (i.e., $S$ per part), after applying the above deductions, each part is floored at $0$, and summing over parts yields a preliminary total score. After that, if the number of written lines is below the minimum line count, each missing line deducts $C$ points from the word-count score, and the overall total is floored at $0$.

If he can get a high-scoring essay, Xiao F will receive a thumbs-up from the teacher. So, please help Xiao F design a plan to maximize the score.

Input Format

• The first line contains $6$ integers: $N, M, L, K, S, C$, as described above.
• The second line contains $N$ integers, where the $i$-th is $a_i$, the length of sentence $i$.
• The next $N - 1$ lines each contain $K$ integers; on the $i$-th of these lines, the $j$-th integer is $s_{i, j}$.

Output Format

Output one non-negative integer on a single line, representing the maximum score you can obtain.

4 4 12 2 10 5
5 5 10 4
2 -1
0 0
1 1

18

2 2 10 1 10 1
1 1
2

9

Hint

Explanation for Sample 1

This is the “no paragraph break” arrangement for Sample 1:

With this arrangement, the score is $10 + 9 - 5 = 14$ points.

We notice the word-count penalty is too heavy, so we must avoid it.

The optimal solution is as follows:

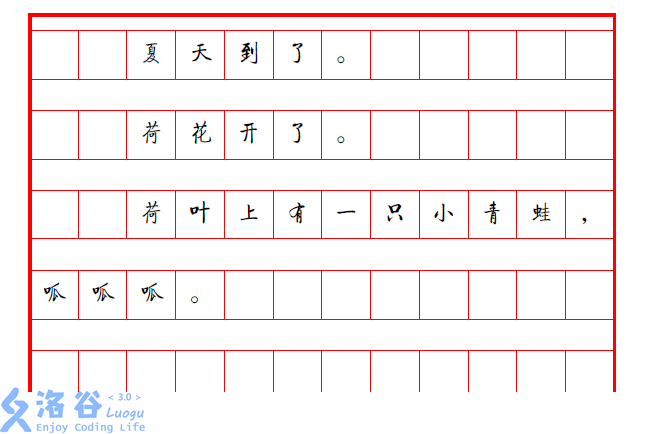
With this arrangement, the score is $8 + 10 - 0 = 18$ points.

Explanation for Sample 2

Even though inserting a break avoids a one-point word-count penalty, it causes a two-point deduction elsewhere, so it is better not to insert a break.

Subtasks

Subtask $1(21 \mathrm{pts})$: $N \leq 10$.

Subtask $2(21 \mathrm{pts})$: $K = 1$.

Subtask $3(31 \mathrm{pts})$: $N \times a_i \leq 800$.

Subtask $4(77 \mathrm{pts})$:

• $1 \leq N, M, a_i \leq 200$.
• $3 \leq L \leq 200$.
• $1 \leq K \leq 5$.
• $0 \leq S, C, |s_{i, j}| \leq 200$.

Translated by ChatGPT 5