#P4710. 「物理」平抛运动
「物理」平抛运动
Output Format
Output one line with two real numbers (each with at most decimal places), which are your answers.
Your answer is considered correct if the absolute or relative error is less than .
14.142136 0.785398
10 5
Hint
Sample Explanation
As shown.
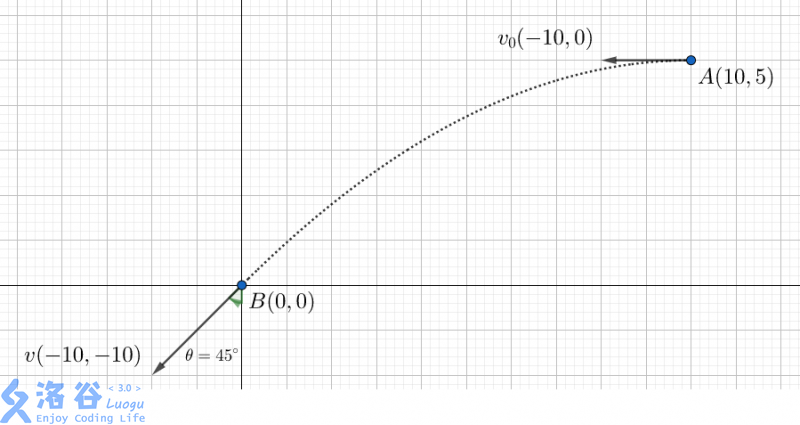
$14.142136 \approx 10 \sqrt 2, 0.785398 \approx \frac \pi 4 = 45 ^ \circ.$
If the ball is thrown from with velocity , then at it hits with velocity .
Hint
If you have not studied the related content, the following may help:
zcy teaches you physics
First, since all units are standard, all results can be computed directly with numbers; treating the object as a point mass means it has no volume.
We can decompose the velocity of the ball as shown:
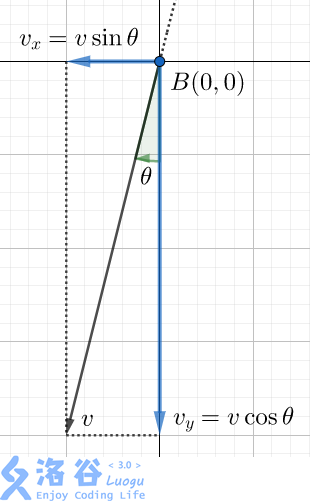
The horizontal component of the velocity is the initial throw speed and remains during the motion.
The vertical component of the velocity is accelerated by gravity, changing from to .
Starting timing from the moment of release, when the time is , let the magnitudes of the horizontal and vertical velocities at this moment be , and the magnitudes of the horizontal and vertical displacements be , respectively. Then:
When is exactly the landing time, are the answers.
About radians:
That is: $\frac \pi 2 = 90 ^{\circ}, \frac \pi 3 = 60 ^{\circ}, \ \cdots$
About trigonometric functions:
If you use C/C++, you can use sin() and cos() from math.h / cmath.
If you use Pascal, you can use sin() and cos() from the math library (add uses math; before begin).
If you use Python, you can use math.sin() and math.cos() from the math library.
If you use other languages, please refer to the corresponding documentation.
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号