#P4687. [IOI 2008] Pyramid Base
[IOI 2008] Pyramid Base
Description
你要在自己财力许可的范围内寻找一个尽可能大的地方,以便兴建一个新的金字塔。为帮助你作出决定,为你提供了土地测绘图。为方便起见,该地块被划分为由个小正方形构成的网格。金字塔的地基部份必须是正方形,而且各边要与这些方格平行。
测绘图中标出了个有可能重叠的障碍物,这些障碍物是上述网格上的长方形,其各边与方格平行。为了建造金字塔,任何塔基所占方格中的障碍物必须被移走。移除障碍物需要付出成本。当移除一个障碍物时,需要将障碍物整个地移除,即不能只移除障碍物的一部份。同时,移除一个障碍物对与其重叠的其他障碍物无任何影响。
已知测绘图中和的大小,对个障碍物的描述,移走每个障碍物的成本以及你的预算。编写程序,找出在移走障碍物总成本不超过的前提下金字塔地基的最大边长。
Input Format
你的程序需要从标准输入上读入以下数据:
- 第一行包含两个以单个空格分隔的整数,分别表示及。
- 第二行包含整数,是你可付出的最大成本(即你的预算)。
- 第三行包含整数,是测绘图中标出的障碍物数量。
- 以下行的每一行表示一个障碍物。其中第 行表示第个障碍物。每一行包含个以单个空格分隔的整数和,分别表示障碍物左下角小正方形的座标,右上角小正方形的座标,以及移除这个障碍物的成本。网格左下角的小正方形座标为,而其右上角小正方形为。
Output Format
你的程序必须向标准输出写出一行,该行只含一个整数,即金字塔基可能的最大边长。如果无法建造任何金字塔,程序应输出0。
6 9
42
5
4 1 6 3 12
3 6 5 6 9
1 3 3 8 24
3 8 6 9 21
5 1 6 2 20
4
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
3
Hint
样例说明
样例1:
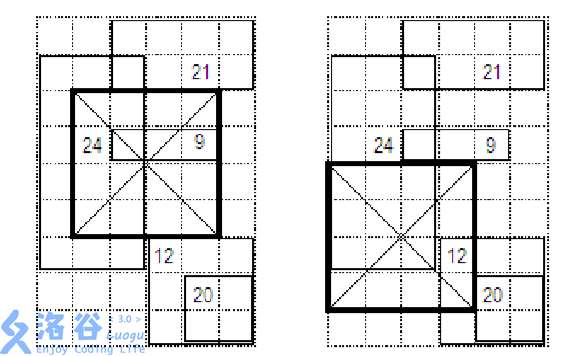
样例2:

数据范围
程序用三组不相交的数据进行评测。以下限制适用于所有的测试数据: 网格的尺寸。 移除障碍物i的成本。 对每个障碍物均有 并且 。
第一组测试总分值35分:
- ——可以付出的最大成本。(不可移除任何障碍物)
- ——网格中障碍物的数目。
第二组测试总分值35分:
-
——你的预算。
-
——网格中障碍物的数目。
第三组测试值30分:
-
——你的预算。(不可以移除任何障碍物)
-
——网格中障碍物的数目。

 京公网安备 11011102002149号
京公网安备 11011102002149号