Description

There are $n$ points $v_i(x_i, y_i)$ on the plane. Find the minimum possible value of $D(l)=\max_{1\le i\le n} dis(v_i, l)$, where the variable $l$ is a line on the plane, and $dis(v_i, l)$ denotes the distance between the line $l$ and the point $v_i$.

Input Format

The first line contains a positive integer $n$. The next $n$ lines each contain a pair of integers $x_i, y_i$, separated by a space, representing the coordinates of the $n$ points in order. Here $|x_i|, |y_i| \le 10^8$, and no two points coincide.

Output Format

Output a single line containing a real number, the minimum value of $D(l)$, rounded to two decimal places.

6
1 0
2 0
3 0
3 2
4 0
5 0

1.00

6
-2 -1
-1 2
1 2
2 3
3 3
4 4

0.86

Hint

Sample Explanation 1

In sample $1$, when the minimum is achieved, the line $l$ is $y=1$.

Sample Explanation 2

In sample $2$, the $6$ points and the line $l$ when $D(l)$ reaches its minimum are shown in the figure.

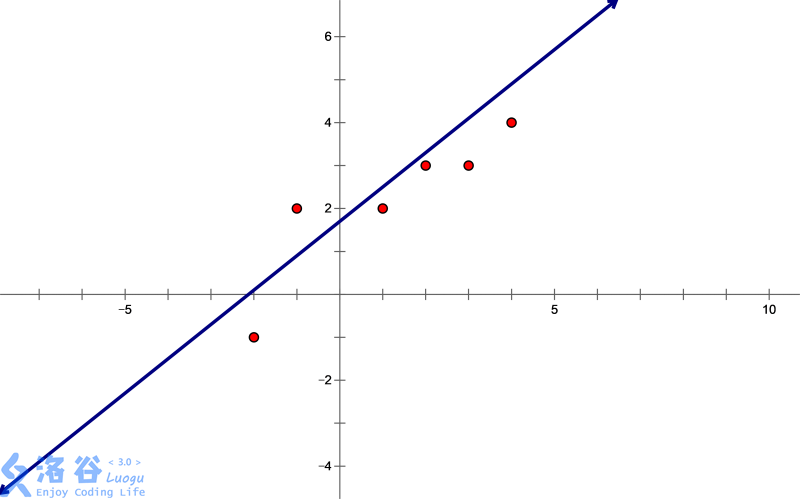
Constraints and Notes

Test case $1$: $n=3$.

Test cases $2 \sim 4$: $3 \le n \le 100$.

Test cases $5 \sim 7$: $100 < n \le 100000$, and the input file is generated as follows: choose a line segment; each time, first pick a point uniformly at random on the segment, then take the lattice point closest to that point.

Test cases $8 \sim 10$: $3 < n \le 100000$.

Translated by ChatGPT 5