Description

In the 2D Cartesian coordinate system, there are $N$ rectangles with masses $m_i$, width $2$, and height $h$, such that:

• The sides of each rectangle are parallel to the coordinate axes.
• The bottom side of each rectangle does not lie on the $x$-axis, and its $y$-coordinate is one of the following values: $0, h, 2h, 3h, \dots, (N-1)h$.
• The lowest rectangle has its lower-left corner at $(-2, 0)$, and its lower-right corner coincides with the origin.

Define the $x$-center of a rectangle as the $x$-coordinate of the midpoint of its bottom side. The $x$-center of one or more rectangles is the weighted average of their $x$-centers, computed as:

$$Xbarycetre=\frac{\sum_{i}m_{i}\times Xcentre(i)}{\sum_{i}m_{i}}$$

Here, Xbarycetre denotes the $x$-center of one or more rectangles, and Xcentre denotes the $x$-center of a rectangle.

In other words, it is the sum of (each rectangle’s mass times its $x$-center) divided by the total mass of the rectangles.

For each rectangle, if the distance between the $x$-center of the rectangles above it and its own $x$-center is at most $1$, then the arrangement formed by these rectangles is called stable.

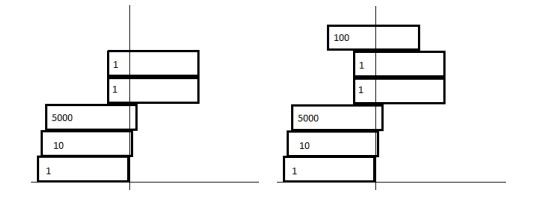
For example, the arrangement in the left picture is unstable because the distance between the $x$-center of the top two rectangles and the $x$-center of the rectangle below them is greater than $1$. The arrangement in the right picture is stable.

Given the masses of all rectangles, find the maximum possible $x$-coordinate of the rectangles in a stable arrangement.

You are not allowed to change the order of the rectangles; they are given from bottom to top.

Input Format

The first line contains an integer $N$, the number of rectangles.

The next $N$ lines each contain an integer $m_i$, the mass of the $i$-th rectangle.

Output Format

Print one real number, the answer. Any answer within an error of $0.000001$ will be accepted.

2 
1 
1

1.00000000

3
1 
1 
1

1.50000000

3 
1 
1 
9

1.90000000

Hint

For $30\%$ of the testdata, the rectangle masses are given in decreasing order.

Constraints: $2\le N\le 3\times 10^{5}$, $1\le m_{i}\le 10^{4}$.

Translated from COCI 2011/2012 #5 T5.

Translated by ChatGPT 5