Description

Jiutiao Kelian (pinyin) is a lazy girl. Because she is too lazy to sweep the floor, she bought a robot vacuum cleaner.

Kelian’s home can be abstracted as an $n \times m$ grid, with coordinates from $(1,1)$ to $(n,m)$. Every night, Kelian starts the robot at $(1,1)$. After being started, the robot follows a preset route and stops when it returns to $(1,1)$ again.

Due to technical reasons, the robot can only move right (column index plus one) or down (row index plus one). To ensure the robot can return to $(1,1)$ smoothly, Kelian installed some corridors such that:

1. If the robot is currently at $(i,m)$, then moving one step to the right takes it to $(i,1)$.
2. If the robot is currently at $(n,i)$, then moving one step down takes it to $(1,i)$.

Kelian hopes that, after starting the robot and before it returns to $(1,1)$, it passes through every cell exactly once. This way the house gets cleaned without taking too much time. After a simple calculation, she quickly obtained all different plans (two plans are different if and only if the orders in which they visit the cells are different). She then loaded all those plans into the robot.

On this day, Kelian bought some new furniture. After placing the furniture, some cells became obstacles that the robot cannot pass. Under all previously prepared plans, the robot will crash into some obstacle and stop.

For a plan $S$, define $f(S)$ as the number of cells the robot passes before it hits an obstacle under that plan. Now Kelian wants to compute the sum of $f(S)$ over all different plans.

Input Format

The input contains multiple test cases.

The first line contains an integer $T$ denoting the number of test cases.

For each test case, the first line contains two integers $n, m$, denoting the size of the house.

Then follow $n$ lines, each containing a binary string of length $m$. In the $i$-th line, the $j$-th character being '0' means the cell $(i,j)$ is not an obstacle; otherwise it is an obstacle.

It is guaranteed that $(1,1)$ is not an obstacle and there is at least one obstacle.

Output Format

For each test case, output a single integer, the answer modulo $998244353$.

2
2 4
0111
1111
2 4
0010
1000

2
5

Hint

Explanation for Sample 2

When $n=2, m=4$, there are two valid plans:

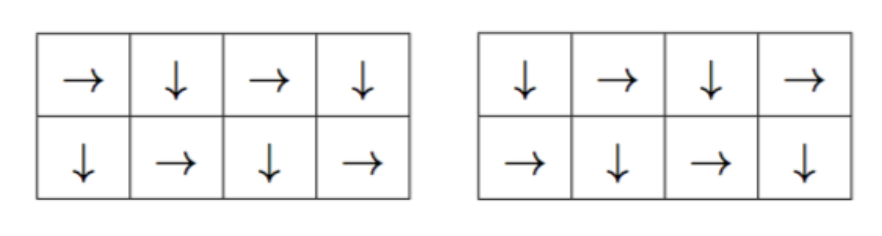
In the first plan, the robot passes a total of 4 cells before it crashes into the obstacle at $(1,3)$.

In the second plan, the robot passes a total of 1 cell before it crashes into the obstacle at $(2,1)$.

Therefore, the answer for the second test case is $1+4=5$.

Constraints

• Testdata 1 $(20\%)$: $n, m \le 4$.
• Testdata 2 $(30\%)$: $n, m \le 50$, and all cells except $(1,1)$ are obstacles.
• Testdata 3 $(50\%)$: $n, m \le 50$.
• For all testdata, $T \le 10; n, m \ge 1$.

Translated by ChatGPT 5