Description

Jiu Tiao Keliang is a girl who loves reading.

In a novel she is reading recently, there is a story about two hostile tribes. The first tribe has $n$ people, and the second tribe has $m$ people. The position of each person can be abstracted as a point with coordinates $(x_i,y_i)$ on the 2D plane.

In the novel, people have a strong sense of territory. For any point on the plane, if it is contained (including the boundary) in a triangle formed by three people from the same tribe (which may degenerate into a line segment), then this point belongs to that tribe’s territory. If there exists a point that lies in the territories of both tribes at the same time, then the two tribes will go to war to fight for that point.

Years of war have exhausted both tribes, so the leader of the second tribe made a wise decision. He plans to choose a vector $(dx,dy)$ and move all his people by this vector, i.e., the coordinates of every person in the second tribe become $(x_i+dx,y_i+dy)$.

Now he has prepared $q$ candidate migration plans. For each plan, he wants you to determine whether, after the migration, the two tribes will still go to war over territory.

Input Format

The first line contains three integers $n,m,q$, denoting the numbers of people in the two tribes and the number of candidate migration plans.

The next $n$ lines each contain two integers $x_i,y_i$, denoting the coordinates of the people in the first tribe.

The next $m$ lines each contain two integers $x_i,y_i$, denoting the coordinates of the people in the second tribe.

The next $q$ lines each contain two integers $dx_i,dy_i$, denoting a migration plan.

The input guarantees that all people’s coordinates are pairwise distinct.

Output Format

For each migration plan, output one integer per line. Output $0$ if no conflict will happen, and $1$ if a conflict will happen.

4 4 3
0 0
1 0
0 1
1 1
-1 0
0 3
0 2
0 -1
0 0
2 3
0 -1

1
0
1

Hint

Sample 1 Explanation

The figure below shows the territories of the two tribes in the first plan. The point $(0,0)$ belongs to both tribes, so a war will happen.

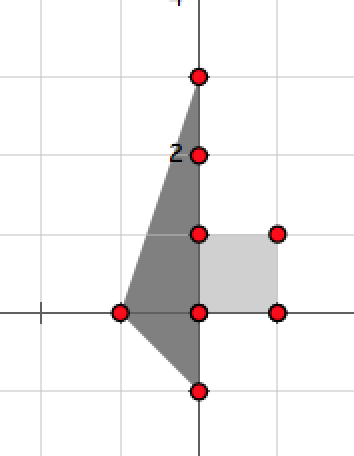
The figure below shows the territories of the two tribes in the second plan. No point belongs to both tribes, so no war will happen.

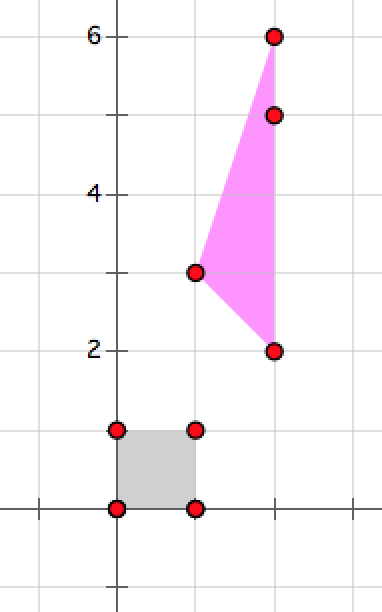
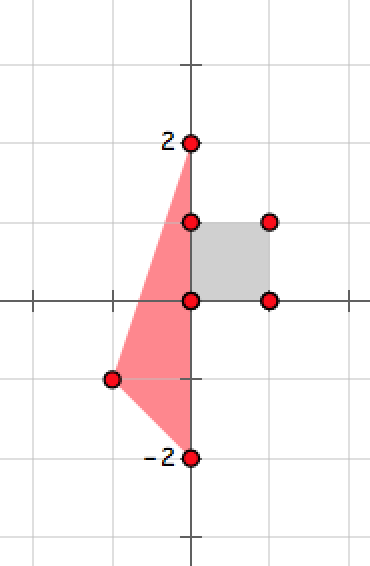
The figure below shows the territories of the two tribes in the third plan. The point $(0,0)$ belongs to both tribes, so a war will happen.

Constraints

For $20\%$ of the testdata, $n,m\le 5,q\le 500$.

For $40\%$ of the testdata, $n,m\le 50,q\le 500$.

For $70\%$ of the testdata, $n,m\le 10^4,q\le 500$.

For $100\%$ of the testdata, $n,m\le 10^5,q\le 10^5$.

For $100\%$ of the testdata, it is guaranteed that $-10^8\le x_i,y_i,dx_i,dy_i\le 10^8$ and $n,m\ge 3$. All people’s coordinates are pairwise distinct, and for each tribe, not all people are collinear.

2024/08/20 Added 6 sets of hack testdata, and made them public in the attachments of this problem.

Translated by ChatGPT 5