题目描述

You are given a histogram consisting of N columns of heights $X_1,X_2,X_N$, respectively. The histogram needs to be transformed into a roof using a series of operations. A roof is a histogram that has the following properties:

• A single column is called the top of the roof. Let it be the column at position $i$.
• The height of the column at position $j\ (1 ≤ j ≤ N)$ is $h_j = h_i- |i - j|$.
• All heights $h_j$ are positive integers.

An operation can be increasing or decreasing the heights of a column of the histogram by $1$. It is your task to determine the minimal number of operations needed in order to transform the given histogram into a roof.

输入格式

The first line of input contains the number $N (1 ≤ N ≤ 10^5$ ), the number of columns in the histogram.

The following line contains $N$ numbers $X_i\ (1 ≤ X_i ≤ 10^9)$, the initial column heights.

输出格式

You must output the minimal number of operations from the task.

题目大意

给定一个长度为 $N$ 的序列 $X$，定义一个屋顶序列为满足以下条件的序列 $H$：

• 序列里恰有一项被称作屋尖。记这一项的下标为 $i$。

• 确定了屋尖后，其他下标为 $j$ 的值 $H_j=H_i-|i-j|$。

• 所有的 $H_j$ 均为正整数。

每次操作，您可以指定序列 $X$ 中的任意一项，将它的值加一或者减一。

请求出使得原序列 $X$ 变成一个屋顶序列的最小的操作次数。

4
1 1 2 3

3

5
4 5 7 2 2

4

6
4 5 6 5 4 3

0

提示

In test cases worth 60% of total points, it will hold N ≤ 5000.

Clarification of the first test case: By increasing the height of the second, third, and fourth column, we created a roof where the fourth column is the top of the roof.

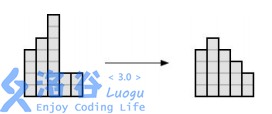
Clarification of the second test case: By decreasing the height of the third column three times, and increasing the height of the fourth column, we transformed the histogram into a roof. The example is illustrated below.