#P4500. [ZJOI2018] 树
[ZJOI2018] 树
Description
Jiutiao Kelian (pinyin) is a girl who loves to write problems.
Although writing problems itself is very interesting, turning a problem into an official contest task is not so fun: generating testdata is always exhausting.
In ZJOI 2018 Day 1, Kelian set a very interesting problem about trees. She plans to use a common method to randomly generate a rooted tree with nodes:
- Node is the root of the tree.
- For , independently and uniformly at random pick a node from as the parent of .
Kelian does not really want to think about whether such randomly generated testdata can defeat brute force, since hacking around is also part of OI contests.
What Kelian cares about more is the problem's discriminative power, and whether all possible scores appear. Therefore, she hopes that the trees in any two test points are different, so that an incorrect program might pass only one of them.
Thus, Kelian wants to compute the probability that, by independently generating rooted trees with nodes to using the method above, they are pairwise isomorphic.
Two rooted trees and with nodes are isomorphic if and only if there exists a permutation of length , satisfying , and for all , if the parent of in is , then the parent of in is .
Input Format
The first line contains three integers , denoting the number of nodes, the number of trees, and the modulus. It is guaranteed that and is prime.
Output Format
Output a single integer, the answer modulo . That is, if the answer in lowest terms is , output .
2 2 998244353
1
3 2 998244353
499122177
4 2 998244353
332748118
10 2 998244353
113919852
50 233 998244353
634280054
Hint
Sample Explanation
In the first sample, the generated tree is unique, so the two generated trees are necessarily identical.
In the second sample, there are only two possible generated trees, and they are non-isomorphic. Therefore, the probability that the two generated trees are isomorphic is , which is modulo .
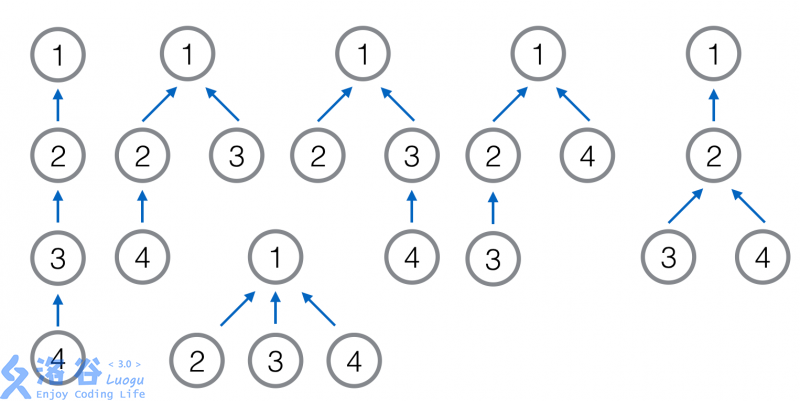
In the third sample, there are possible generated trees, as shown below. Among them, the second, third, and fourth (the middle three in the first row) are isomorphic, and the remaining ones are pairwise non-isomorphic. Therefore, the probability that the two generated trees are isomorphic is , which is modulo .
Constraints
| 测试点 | 测试点 | ||||
|---|---|---|---|---|---|
| 1 | 6 | ||||
| 2 | 7 | ||||
| 3 | 8 | ||||
| 4 | 9 | ||||
| 5 | 10 |
For of the testdata, it is guaranteed that is prime and .
Thanks to @Xeonacid for providing the statement.
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号