Description

Fei Fei Country is a legendary land, and its residents are called "Fei Fei Xia" (pinyin).

Fei Fei Country is an $N\times M$ rectangular grid, where each cell represents a block.

However, there is no transportation in Fei Fei Country. Fei Fei Xia move entirely using ground-based launch devices.

Every block is equipped with a launch device. Using a launch device requires paying a certain fee, and each device has its own launching capability.

Let the launch device at row $i$, column $j$ have a fee $A_{i,j}$ and a launching capability $B_{i,j}$. We define the distance between two cells sharing an edge to be $1$. Then, any Fei Fei Xia only needs to pay $A_{i,j}$ at $(i, j)$ to jump to any position whose distance from $(i, j)$ is no more than $B_{i,j}$. See the figure below. 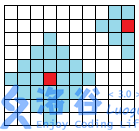(After paying at the red block, one can jump to any blue block around it.)

The problem is simple. There are three Fei Fei Xia, named $X, Y, Z$. They decide to gather to play and want to meet at one of their positions. Given the coordinates of the $3$ Fei Fei Xia, find at which person’s position they should gather to minimize the total cost for all of them. If the minimal costs are the same, prefer $X$ first, then $Y$.

Description

Input Format

The first line contains two integers $N$ and $M$, representing the number of rows and columns.

Next are two $N\times M$ matrices of natural numbers, giving $B_{i,j}$ and $A_{i,j}$.

The last line contains six numbers, representing the row and column indices of the locations of $X, Y, Z$.

Output Format

On the first line, output a single character $X$, $Y$ or $Z$, indicating the optimal meeting person.

On the second line, output an integer, the minimal total cost.

If gathering is impossible, output only one line NO.

4 4
0 0 0 0
1 2 2 0
0 2 2 1
0 0 0 0
5 5 5 5
5 5 5 5
5 5 5 5
5 5 5 5
2 1 3 4 2 2

Z
15

Hint

Constraints:

• For $20\%$ of the testdata, $N, M \leq 10$, $B_{i,j} \leq 20$.
• For $40\%$ of the testdata, $N, M \leq 100$, $B_{i,j} \leq 20$.
• For $100\%$ of the testdata, $1 \leq N, M \leq 150$, $0 \leq B_{i, j} \leq 10^9$, $0 \leq A_{i, j} \leq 1000$.

Translated by ChatGPT 5