Description

There are $n$ north–south two-way streets and $n$ east–west two-way streets forming a grid. The distance between any two adjacent streets (regardless of orientation) is $L$ miles. The southwest corner intersection has coordinates $(1, 1)$, and the northeast corner is $(n, n)$. At any intersection, you may change direction arbitrarily. Each street has its own speed limit, which applies to the entire street regardless of travel direction.

Your task is to drive from intersection $(x_s, y_s)$ to $(x_t, y_t)$. You may change speed only at intersections; you must not violate the speed limit of the street you are currently on; you may only travel along paths of minimal length; and the total travel time must lie within the closed interval $[t_1, t_2]$. Speed is measured in miles per hour and must be a positive multiple of $5$. If the speed is $v$, then the miles per gallon is $80 - 0.03 v^2$.

Input Format

• The first line contains two integers $n, L$.
• The second line contains $n$ positive integers, giving the speed limits of the $n$ east–west streets from south to north.
• The third line contains $n$ positive integers, giving the speed limits of the $n$ north–south streets from west to east.
• The fourth line contains six integers $x_s, y_s, x_t, y_t, t_1, t_2$.

Output Format

If there is no solution, output No.

Otherwise, output two lines describing, respectively, the earliest-arrival plan (if multiple, choose the most fuel-efficient among them) and the most fuel-efficient plan (if multiple, choose the earliest-arrival among them). Each plan is represented by two numbers: the arrival time in minutes (ceiling to the next integer), and the fuel consumption in gallons (rounded to two decimal places).

6 20
30 40 50 50 50 50
50 50 50 50 50 40
1 1 6 6 300 320

300 6.25
318 5.60

8 2
10 20 20 30 10 20 10 10
10 20 20 30 10 20 10 20
6 8 2 4 10 39

No

Hint

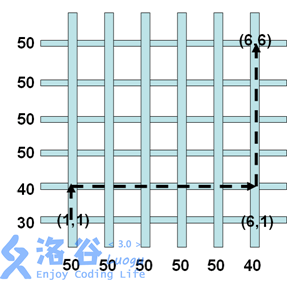
In Sample 1, the fastest route travels at a constant speed of $40$ miles per hour, with a total distance of $200$ miles, so the time is $5$ hours. The miles per gallon is $80 - 0.03 \times 40 \times 40 = 32$, so the fuel consumption is $200 / 32 = 6.25$ gallons.

The most fuel-efficient route first travels $120$ miles at $40$ miles per hour, then $80$ miles at $35$ miles per hour, for a fuel consumption of $120 / 32 + 80 / \bigl(80 - 0.03 \times 35 \times 35\bigr) = 5.60$ gallons. The route in the figure satisfies both plans (the second plan changes speed at $(6, 2)$).

Constraints:

• 20% of the testdata satisfy: $n \le 4$.
• 50% of the testdata satisfy: $n \le 8$.
• 100% of the testdata satisfy: $1 \le n \le 10$, $1 \le L \le 20$, $0 \le t_1 \le t_2 \le 1000$. Speed limits do not exceed $50$.

Translated by ChatGPT 5