#P4382. [八省联考 2018] 劈配
[八省联考 2018] 劈配
Description
Skilled as usual, Zayid smoothly passed the open auditions. The next stage is the mentors' blind selection, with rules as follows:
There are contestants in total (numbered from to ). Each writes a piece of code and presents their dream. Then all mentors rank these contestants. To avoid future trouble, it is required that there are no ties in the rankings.
At the same time, each contestant independently fills out a preference form to evaluate the mentors (numbered from to ). The form contains preference tiers. For each tier, the contestant may list at most mentors, and each mentor may be listed at most once by each contestant (skipping some mentors is allowed).
After both sides finish, admissions are carried out. Each mentor has an upper bound on their team size, which means some contestants' higher preferences, or even all their preferences, may not be met. The show defines "the result for the top contestants is optimal" as follows:
-
The result for the top contestant is optimal if and only if contestant is admitted to their highest nonempty preference (in particular, if contestant did not submit a preference form, then this contestant is eliminated).
-
The result for the top contestants is optimal if and only if, given that the result for the top contestants is optimal, contestant is admitted to the highest preference that is theoretically possible (in particular, if contestant did not submit a preference form, or if all mentors in their preferences are already full, then this contestant is eliminated).
If a scheme satisfies "the result for the top contestants is optimal," we simply call this scheme optimal.
For example, there are mentors, Teacher and Teacher , each with a team size cap of ; there are contestants, Zayid and DuckD, ranked and , respectively. Then the following preference forms and their corresponding optimal admission results are as shown in the tables:
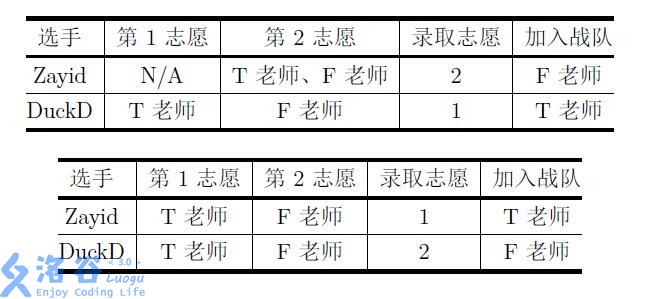
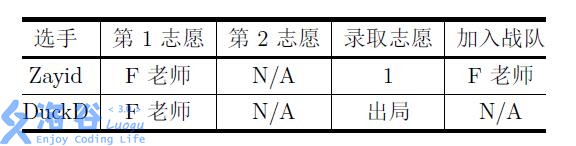
It can be proved that, for the above preference forms, the corresponding schemes are the unique optimal admission results.
Everyone has an ideal value , meaning that contestant hopes to be admitted to their -th or better preference; otherwise, they will be very disappointed.
Now all contestants' preference forms and rankings have been published. Coincidentally, each contestant's ranking exactly matches their ID.
For each contestant, Zayid wants to know the answers to the following two questions:
-
In the optimal admission scheme, to which preference tier will they be admitted?
-
With other contestants' relative order unchanged, by at least how many ranks must they climb so that they are not disappointed?
As a top-notch coder on "China's New Code," Zayid certainly solved this problem easily. But he still wants you to compute it again to verify his result.
Input Format
Each test point contains multiple testcases. The first line contains non-negative integers separated by a space, representing the number of testcases and the maximum number of mentors allowed per preference tier, respectively.
Then for each testcase:
- The first line contains two positive integers separated by a space.
denote the number of contestants and the number of mentors, respectively.
- The second line contains positive integers separated by spaces: the -th integer is .
is the team size upper bound of mentor .
Lines to each contain non-negative integers: in line , the -th number from the left is .
means contestant placed mentor as their -th preference. In particular, if , it means this contestant did not include this mentor on the form.
In this part, it is guaranteed that within each row no positive number appears more than times ( may appear more than times), and all .
- Line contains positive integers separated by spaces, where the -th integer is .
is the ideal value of contestant .
In this part, it is guaranteed that .
Output Format
Output the answers for each testcase in order. For each testcase, output lines:
-
The first line contains positive integers separated by spaces. The -th integer means:
the preference tier to which contestant will be admitted in the optimal scheme.
In particular, if this contestant is eliminated, this number is .
-
The second line contains non-negative integers separated by spaces. The -th integer means:
the minimum number of ranks contestant must climb so as not to be disappointed.
In particular, if this contestant will certainly be disappointed, this number is .
3 5
2 2
1 1
2 2
1 2
1 1
2 2
1 1
1 2
1 2
2 1
2 2
1 1
0 1
0 1
2 2
2 1
1 0
1 2
0 1
1 3
0 1
1 5
4 3
2 1 1
3 1 3
0 0 1
3 1 2
2 3 1
2 3 3 3
1 1 3 2
0 0 0 0
Hint
- Explanation for Sample :
The three datasets correspond to the three tables in the Description.
For the first dataset: because contestant did not list any first preference, they definitely cannot be admitted to their first preference tier and will definitely be disappointed. Contestant is not disappointed with the original ranking, so they do not need to improve their rank.
For the second and third datasets: contestant does not need to improve their rank. Aiming for first preference, contestant must rise to rank to get their wish.
- Explanation for Sample :
Contestant listed only mentor as first preference, so contestant must be admitted by mentor .
Contestant listed only mentor as first preference, so contestant must be admitted by mentor .
Since mentors and are full, and contestants and both listed mentor , they will both be admitted by mentor .
Therefore, contestants and are both admitted to their -st preference, contestant is admitted to their -rd preference, and contestant is admitted to their -nd preference.
Since they all get what they want, none of them needs to improve their rank.
| Test point ID | Other conditions | |||
|---|---|---|---|---|
| 1 | None | |||
| 2 | ||||
| 3 | None | |||
| 4 | ||||
| 5 | None | |||
| 6 | ||||
| 7 | None | |||
| 8 | ||||
| 9 | ||||
| 10 | None | |||
-
For all test points, it is guaranteed that .
-
Across all data of all test points, it is guaranteed that .
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号