Description

After IOI 2018 comes the interview for the "Yao Class". But you, because you dislike physics and want to become an entrepreneur like Steve Jobs, are successfully kicked back to the CS Department.

In the blink of an eye, the clock points to 2019, sophomore year, early December, finals week.

You had long heard seniors say that the midterm exam for Data Structures is hard, unfriendly to competitive programmers, and even training team members cannot finish the paper.

You sneer. Hmph, as an IOI gold medalist, what’s so hard about this exam.

In two hours, you read all content of the first five chapters of the solution manual and can recite it backwards.

In one hour, you read a 500-page handout and remember it vividly.

In ten minutes, you bike to the exam room. Confidently, you bring only a pen, even though it’s an open-book exam.

Now, you unfold the legendary god-tier paper, take a deep breath, and see—

Given a sequence of length $N$, $A_1, A_2, \cdots, A_N$. If a subsequence $B_1, B_2, \cdots, B_M$ of $A$ satisfies:

$1 \le M \le N$

∀$1 \le i \le M$，$B_i$|$B_{i+1}$

then we call $B$ an "increasing multiple subsequence" of $A$.

Now there is a sequence $A$ of length $N$ initialized as $A_{1}, A_{2}, \cdots, A_{N}$, and there are $Q$ operations on $A$. You are required to implement the following four operations:

0 x: Insert a number $x$ at the left end of sequence $A$.

1 x: Insert a number $x$ at the right end of sequence $A$.

2: Remove one number from the left end of sequence $A$.

3: Remove one number from the right end of sequence $A$.

After initializing sequence $A$ and after each operation, compute the length $\mathrm{MaxLen}$ of the longest increasing multiple subsequence in the current $A$, and the number $\mathrm{Cnt}$ of distinct starting numbers among all increasing multiple subsequences of length $\mathrm{MaxLen}$. Output $\mathrm{MaxLen}$ and $\mathrm{Cnt}$.

To drastically reduce the difficulty, it is guaranteed that the sequence $A$ is non-empty at any time, its elements are all distinct, and all elements are positive integers between $1 \sim M$. Each same number will be inserted at most $C$ times.

Input Format

The first line of input contains three positive integers $N, M, Q$ as described above. It is guaranteed that $1 \le N \le 10^5$, $N \le M \le 10^6$, $0 \le Q \le 10^5$.

The second line contains $N$ positive integers, which are $A_1, A_2, \cdots, A_N$. It is guaranteed that $1 \le A_i \le M$, and all elements in sequence $A$ are distinct.

Then there are $Q$ lines. Each line is in one of the following formats: 0 x, or 1 x, or 2, or 3, with meanings as described above.

Output Format

Output $Q+1$ lines. After initialization and after each operation on sequence $A$, output the length $\mathrm{MaxLen}$ of the longest increasing multiple subsequence in $A$ and the number $\mathrm{Cnt}$ of distinct starting numbers among all increasing multiple subsequences of length $\mathrm{MaxLen}$, separated by a single space.

5 10 10
1 2 5 9 10
2
1 7
3
3
0 8
3
2
1 8
3
0 3

3 1
2 2
2 2
2 2
1 3
1 4
1 3
1 2
2 1
1 2
1 3

Hint

Sample explanation.

In the table, different longest increasing subsequences are separated by //.

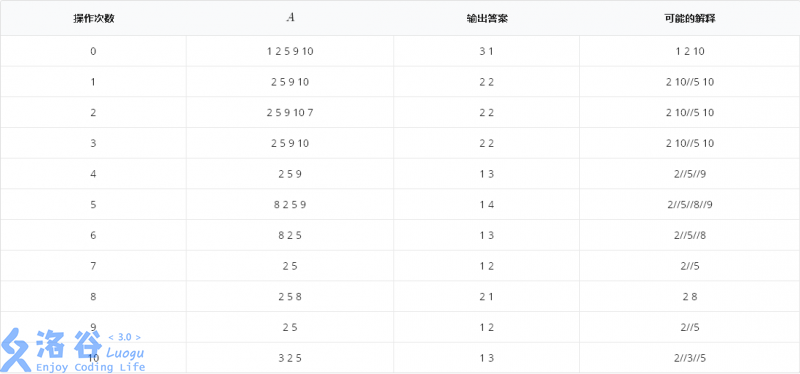
For all testdata, $1 \le N \le 10^5$, $N \le M \le 10^6$, $0 \le Q \le 10^5$, $1 \le A_i \le M$, $C = 10$.

The table below shows some special constraints for certain data points. Here, “only 1” means only operations of the form 1 x; similar statements apply to the others.

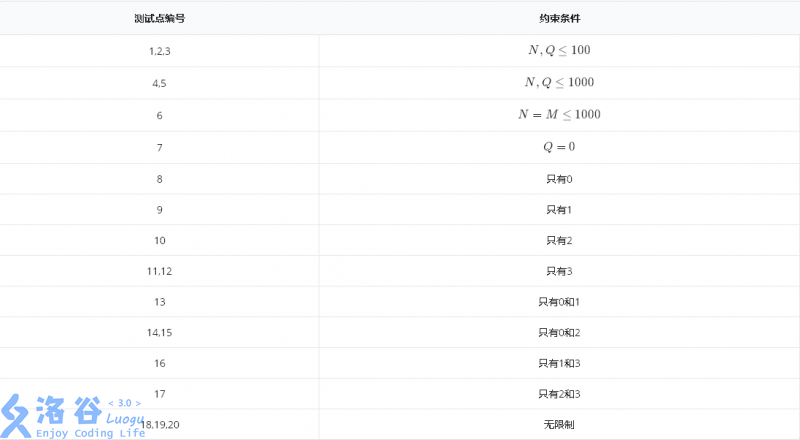
Postscript.

The meme “fight for two hours, score forty or fifty” has taken over your social feed:

“Ah, I feel like my life is complete.”
“I hope... I can really get forty or fifty.”
“I finished the exam... Finished... Doomed.”
“I used to think it was a joke, turns out I was still naïve.”

You sneer. You hand in the paper half an hour early, naturally thinking: Data Structures, full score, as expected.

Translated by ChatGPT 5