Description

Li Zhe really loves lemon trees, especially on quiet nights when a crescent moon gently illuminates the ground. He always sits leisurely by the lemon tree he planted himself, pondering the philosophy of life.

Li Zhe likes thinking. When he sees the lemon tree casting a sharp shadow on the ground under the moonlight, he immediately comes up with a question: what is the area of the tree’s shadow?

He knows that directly measuring the area is hard. He wants to compute it geometrically, because he understands the shape of this lemon tree very well and has a plan to simplify it.

Li Zhe divides the whole lemon tree into $n$ layers, numbered from bottom to top as $1, 2, \ldots, n$. From layer $1$ to layer $n-1$, each layer is a conical frustum, and layer $n$ (the topmost layer) is a cone. For a conical frustum, its top and bottom faces are horizontal circles. For two adjacent frustums, the lower base of the upper layer coincides with the upper base of the lower layer. The base of the cone in layer $n$ (the topmost layer) is exactly the upper base of the frustum in layer $n-1$. The centers of all circular bases (including the tree top) lie on a straight line perpendicular to the ground. Li Zhe knows the height of each layer $h_1, h_2, \ldots, h_n$, the height of the lower base of the first frustum above the ground $h_0$, and the radius of the lower circular base of each layer $r_1, r_2, \ldots, r_n$. Using a familiar method, he measured the angle between the moonlight rays and the ground to be $\mathrm{alpha}$.

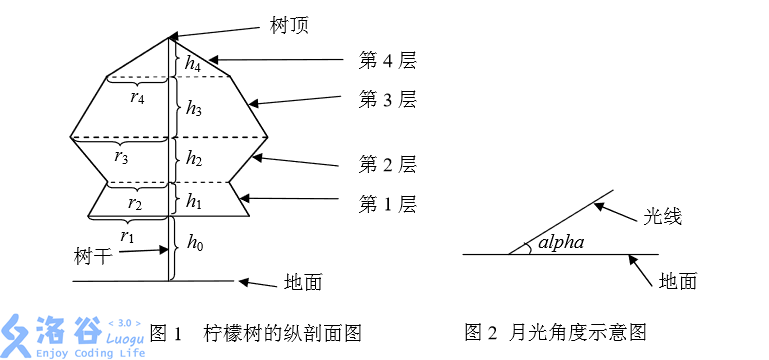
For convenience, assume the moonlight rays are parallel, the ground is horizontal, and ignore the shadow cast by the trunk. Of course Li Zhe can compute it, but he hopes you will give it a try too.

Input Format

The first line contains an integer $n$ and a real number $\mathrm{alpha}$, representing the number of layers of the lemon tree and the angle between the moonlight rays and the ground (in radians).

The second line contains $n+1$ real numbers $h_0, h_1, h_2, \ldots, h_n$ representing the tree’s height above the ground and the height of each layer.

The third line contains $n$ real numbers $r_1, r_2, \ldots, r_n$ representing the radius of the lower circular base of each layer of the lemon tree.

Adjacent numbers on the same line are separated by a single space.

All real numbers in the input may have between 1 and 10 digits after the decimal point.

Output Format

Output a single real number: the area of the tree’s shadow, rounded to two decimal places.

2  0.7853981633 
10.0  10.00  10.00 
4.00  5.00

171.97

Hint

For $10\%$ of the testdata, $n \leq 1$.

For $30\%$ of the testdata, $n \leq 2$.

For $60\%$ of the testdata, $n \leq 20$.

For $100\%$ of the testdata, $1 \leq n \leq 500$, $0.3 < \mathrm{alpha} < \frac{\pi}{2}$, $0 < h_i \leq 100$, $0 < r_i \leq 100$.

Translated by ChatGPT 5