Description

Given an undirected, weighted, connected graph $G$, we want to modify edge weights so that its minimum spanning tree is unique. The unit costs to decrease and increase the weight of an edge by 1 are $a$ and $b$, respectively, and the modified weights must be non-negative integers.

For example, for some graph $G$, if after decreasing the weight of one edge by $3$ and increasing the weight of another edge by $2$ the minimum spanning tree becomes unique, then the total cost is $3a+2b$. Compute the minimal total cost.

Input Format

Read from standard input.

The first line contains the string “$mst$” and a testdata ID.

The second line contains 4 positive integers $n$, $m$, $a$, $b$, denoting the number of vertices of $G$, the number of edges, and the unit costs to decrease an edge weight by $1$ and to increase it by $1$, respectively.

Each of the next $m$ lines contains 3 positive integers $x$, $y$, $w$, indicating that there is an edge between vertices $x$ and $y$ with initial weight $w$.

Vertices are numbered from $1$ to $n$.

Output Format

Write to standard output.

Output a single line containing one integer, the minimal total cost. If no modification is needed, output $0$.

mst 0
4 5 2 3
1 2 1
1 3 1
2 3 1
2 4 2
3 4 2

5

Hint

[Sample explanation]

After decreasing the weight of edge $(2,4)$ by $1$ and increasing the weight of edge $(2,3)$ by $1$, the minimum spanning tree of graph $G$ becomes unique, and the total cost is minimal.

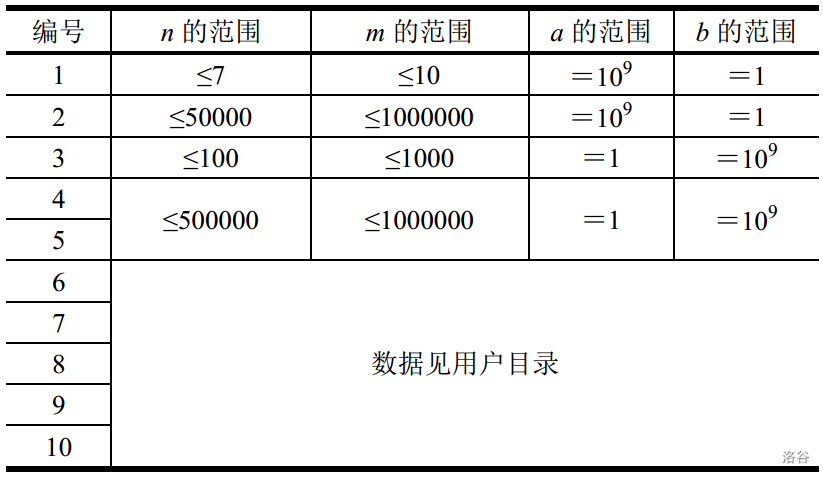
[Constraints]

Test points $6$~$10$ download

Translated by ChatGPT 5