Description

The problem is as follows:

A sequence $a$ is called a generalized Fibonacci sequence if it satisfies $a_n = a_{n-1} + a_{n-2}$ for $n \ge 3$, and $a_1, a_2$ are arbitrary real numbers.

Now please count how many generalized Fibonacci sequences satisfy $a_1 = i$, $a_2$ is an integer in the interval $[l, r]$, and $a_k \bmod p = m$.

Input Format

Read from standard input.

This problem contains multiple test cases. The first line contains a positive integer $T$, the number of test cases. For each test case:

One line with six space-separated integers: i, l, r, k, p, m, whose meanings are as defined in the Description.

Output Format

Write to standard output.

Output $T$ lines. Each line contains a single number, the answer for that test case.

6
2 17 68 3 23 1
1 17 68 3 57 1
5 17 68 10 11 9
5 17 68 10 71 9
10 17 68 11 12 3
10 17 68 8 6 4

3
1
4
1
5
9

Hint

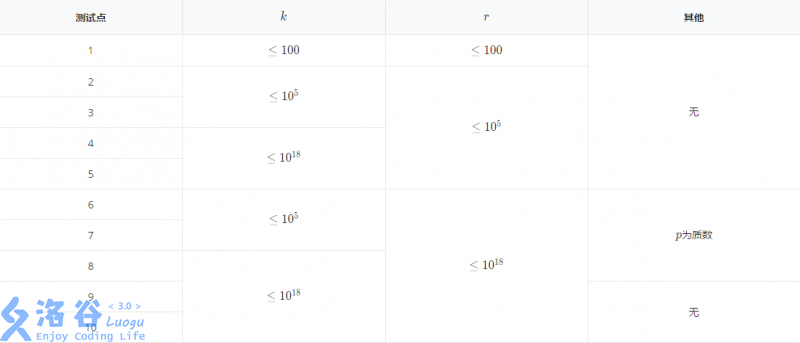
Constraints: For all testdata, $0 \le l \le r$, $1 \le p \le 10^9$, $0 \le m < p$, $T = 10$, $0 \le i \le 10^{18}$, $k \ge 3$.

From the CodePlus 2017 December Contest, proudly presented by the Student Association for Algorithms and Programming Competitions, Department of Computer Science and Technology, Tsinghua University.

Credit: idea/卢政荣 (Lu Zhengrong), problem setting/卢政荣 (Lu Zhengrong), verification/吕时清 (Lü Shiqing), 茹逸中 (Ru Yizhong), 王聿中 (Wang Yuzhong).

Git repo: https://git.thusaac.org/publish/CodePlus201712

We thank Tencent for supporting this contest.

Translated by ChatGPT 5