#P3767. 魔法
魔法
Description
The magic array consists of nodes.
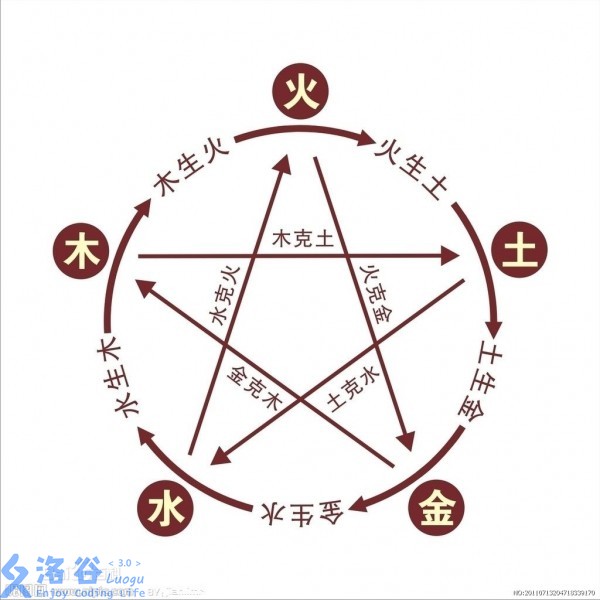
Each node can have one of five attributes: metal, wood, water, fire, earth. They satisfy the generate/overcome relationships.
At the beginning, there are no spells in the magic array.
Each time, Xiao Y will add a spell that requires the attributes of two nodes to satisfy a generate/overcome relationship. Then you need to answer whether there exists an assignment of an attribute to each node that satisfies all the requirements.
To adjust the array, Xiao Y sometimes needs to delete a previously written spell.
Xiao Y thinks this problem is too easy, so he uses the ability to change the timeline, making each operation be applied on the magic array resulting right after some previous operation.
Input Format
The first line contains two positive integers , the number of nodes and the number of operations.
Then follow lines, each containing four numbers describing one operation.
The first number means this operation is applied to the magic array obtained right after the -th operation. If , it is applied to the initial magic array.
The second number indicates the operation type.
- : then input , meaning to add a spell requiring generates .
- : then input , meaning to add a spell requiring overcomes .
- : then input , meaning to delete the spell added by the -th operation.
Output Format
For each operation, if after the operation there exists an assignment of attributes to all nodes that satisfies all the requirements, output excited; otherwise, output naive.
3 6
0 1 1 2
1 1 2 3
2 2 1 3
2 1 3 1
2 3 1
5 1 3 1
excited
excited
excited
naive
excited
excited
Hint
For of the testdata, .
For another of the testdata, .
For of the testdata, , , , , and all delete operations are guaranteed to be valid.
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号