Description

Since the last time the divine knife master helped Earthworm Country gain tens of millions of citizens (earth-citizens?), the country has become more and more prosperous! Recently, they discovered some magical papers underground. After careful study, it turned out to be the design blueprints of a supercomputer in City X of Country D!

This computer is called the "Tree Diagram." It consists of $n$ computing nodes connected by $n - 1$ bidirectional communication links, and all computing nodes are labeled with positive integers not exceeding $n$. As the name suggests, this forms a tree structure.

The Earthworm King has fully mastered the information of this tree from the blueprints, including the value of $n$ and the connectivity of the $n - 1$ links. He decided to send the two most powerful hackers of Earthworm Country, P and H, to infiltrate the "Tree Diagram" and destroy it as much as possible.

P and H are masters of the world's best programming language. After some discussion, they decided to proceed in the following steps:

• P chooses a computing node as his starting point and adds a P mark to that node.
• Repeat the following operation any number of times (possibly $0$ times):
  • From his current computing node, P chooses a link that has not been marked, infiltrates to the computing node at the other end of that link, and adds a P mark to both the traversed link and the destination node.
• H chooses a computing node as her starting point and adds an H mark to that node.
• Repeat the following operation any number of times (possibly $0$ times):
  • From her current computing node, H chooses a link that has not been marked, infiltrates to the computing node at the other end of that link, and adds an H mark to both the traversed link and the destination node. (Note: H cannot traverse links that have a P mark, but she may traverse nodes that have a P mark.)
• Delete all computing nodes and links that have been marked.
• For each remaining link, if one or both endpoints were deleted in the previous step, delete that link as well.

After these operations, the "Tree Diagram" will be disconnected into several (possibly $0$) connected components. To maximize the damage, the Earthworm King hopes that the number of connected components is as large as possible. He turns to you to compute this maximum number.

P and H are very impatient, and before you compute the plan, they may have already computed the optimal plan or part of it. You are given a value $x$:

• If $x = 0$, then P and H have not computed the optimal plan. You need to determine the infiltration routes for both of them.
• If $x = 1$, then P has already computed his infiltration route in some optimal cooperative plan. He will choose the starting point $p_0$ and infiltrate along links to the target point $p_1$, and then he will stop infiltrating. You only need to determine H’s infiltration route.
• If $x = 2$, then P and H have computed an optimal cooperative plan. P infiltrates from $p_0$ to $p_1$ and stops, and H infiltrates from $h_0$ to $h_1$ and stops. In this case, you do not need to direct their infiltration; you only need to compute the number of connected components remaining after the last two deletion steps.

Input Format

Each input file contains multiple datasets. The first line contains two integers $T$ and $x$, where $T$ is the number of datasets in the file, and the meaning of $x$ is as described above. (The same $x$ applies to all datasets in the same input file.)

Then, for each dataset in order:

• If $x = 0$: the first line of the dataset contains a single integer $n$.
• If $x = 1$: the first line of the dataset contains three integers $n, p_0, p_1$.
• If $x = 2$: the first line of the dataset contains five integers $n, p_0, p_1, h_0, h_1$.

This is followed by $n - 1$ lines, each containing two positive integers not exceeding $n$, indicating that there is a link connecting the two nodes with those labels. The input is guaranteed to form a tree.

Adjacent integers on the same line are separated by exactly one space.

Output Format

For each dataset, output one line containing the maximum possible number of connected components remaining under the given conditions.

1 0
13
1 2
2 3
2 4
4 5
4 6
4 7
7 8
7 9
9 10
10 11
10 12
12 13

8

8 0
1
2
1 2
3
1 2
2 3
4
1 3
2 3
2 4
5
1 5
2 5
3 5
4 5
16
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 17
17 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
17
8 6
2 6
11 6
4 6
14 2
10 2
5 4
1 4
9 8
17 11
12 5
3 6
13 6
16 8
7 11
15 16

0
1
2
2
4
12
13
10

8 1
1 1 1
2 1 1
1 2
3 2 2
1 2
2 3
4 2 2
1 3
2 3
2 4
5 5 5
1 5
2 5
3 5
4 5
16 1 5
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
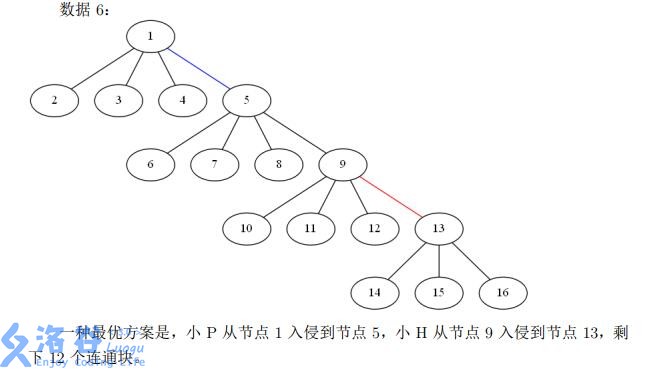
17 1 5
1 2
1 3
1 4
1 5
5 6
5 7
5 8
5 17
17 9
9 10
9 11
9 12
9 13
13 14
13 15
13 16
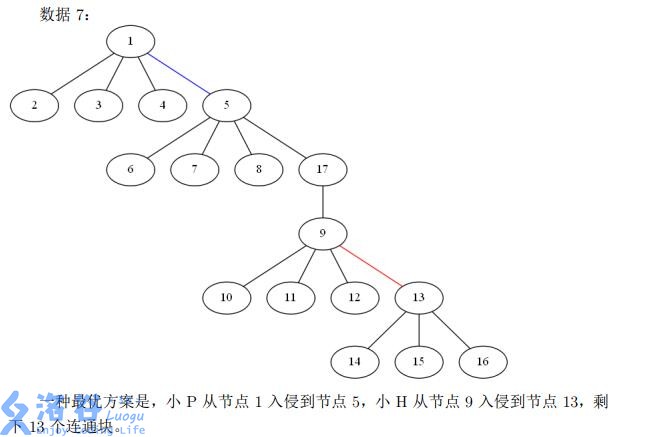
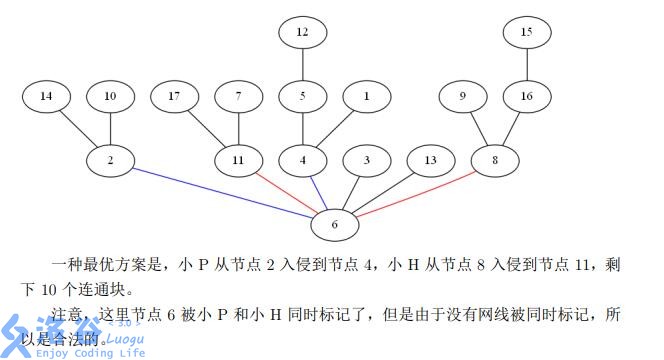
17 2 4
8 6
2 6
11 6
4 6
14 2
10 2
5 4
1 4
9 8
17 11
12 5
3 6
13 6
16 8
7 11
15 16

0
1
2
2
4
12
13
10

Hint

The values $p_0, p_1, h_0, h_1$ are guaranteed to be positive integers not exceeding $n$.

The data file may be large; please avoid overly slow input/output methods.

[Sample 1 Explanation]

This input file contains only one dataset. One optimal plan is as follows:

• P starts infiltrating from node $2$, and node $2$ is marked by P.
• P infiltrates from node $2$ to node $4$, and node $4$ and the traversed link are marked by P.
• P infiltrates from node $4$ to node $7$, and node $7$ and the traversed link are marked by P.
• H starts infiltrating from node $10$, and node $10$ is marked by H.
• Delete the marked nodes $2, 4, 7, 10$ and the marked links $(2, 4)$ and $(4, 7)$.
• Delete any link with at least one endpoint deleted in the previous step.

At this point, there are $8$ connected components remaining. Nodes $1, 3, 5, 6, 8, 9, 11$ each form a connected component of their own, and nodes $12, 13$ form one connected component.

[Sample 2 Explanation]

• Dataset 1: There is only $1$ computing node. The only feasible plan is that P starts from node $1$ (and stops immediately), and H also infiltrates from node $1$ to node $1$. All nodes are deleted, leaving $0$ connected components.
• Dataset 2: One optimal plan is that P infiltrates from node $1$ to node $1$, and H also infiltrates from node $1$ to node $1$. After the deletions, $1$ connected component remains (only node $2$).
• Dataset 3: The only optimal plan is that P infiltrates from node $2$ to node $2$, and H also infiltrates from node $2$ to node $2$, leaving $2$ connected components.
• Dataset 4: One optimal plan is that P infiltrates from node $2$ to node $2$, and H also infiltrates from node $2$ to node $2$, leaving $2$ connected components.
• Dataset 5: The only optimal plan is that P infiltrates from node $5$ to node $5$, and H also infiltrates from node $5$ to node $5$, leaving $4$ connected components.

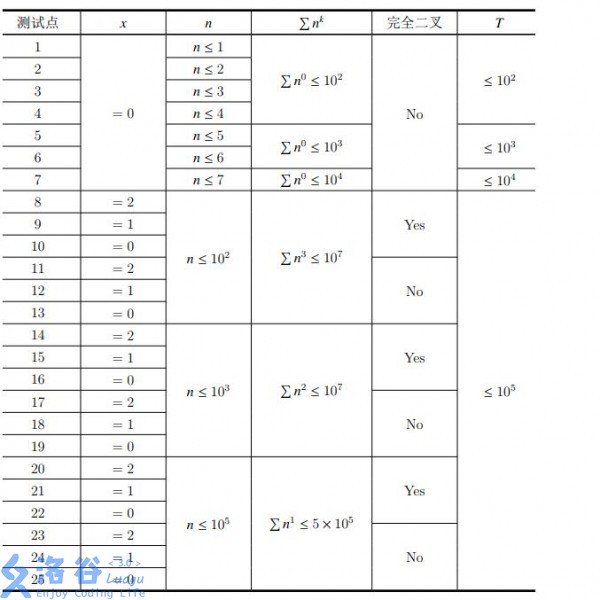
For an integer $k$, let $\sum n^k$ denote the sum of $n^k$ over the $T$ datasets in an input file.

Constraints for all data: $T \leq 10^5$, $\sum n^1 < 5 \times 10^5$.

Please pay attention to initialization time complexity to avoid timeouts when there are many small datasets.

For each test point, the detailed constraints are shown in the table below. If “Complete Binary” is Yes in the table, then each dataset in the input file satisfies: on the $j$-th line of the link list $(1 \leq j < n)$, the two numbers given are $\left\lfloor \frac {j + 1} {2} \right\rfloor$ and $j + 1$, respectively.

Translated by ChatGPT 5