#P3630. [APIO2010] 信号覆盖
[APIO2010] 信号覆盖
Description
A telecom company is building a GSM network in Beijing. There are houses in the city that need signal coverage. Due to budget constraints, the company can install only one antenna. Each house is represented by a point in the plane.
To simplify placement, the company will choose 3 houses and take their circumcircle, then place the antenna at the center of that circle. Every house that lies on or inside this circle will be covered by the antenna.
The company will choose 3 houses uniformly at random from all houses in the city. They want to know, over all possible antenna placements, the average number of houses that will be covered.
For example, suppose there are 4 houses , positioned as in the figure:
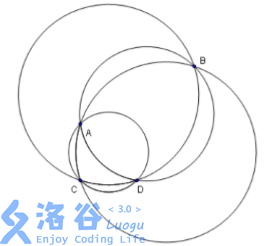
If we choose the circumcircle of or , then all houses are covered. If we choose or , the remaining house will not be covered. Therefore, the average is .
Given the positions of all houses, your task is to compute the average number of houses covered. Assume every house has integer 2D coordinates, no three houses are collinear, and no four houses are cocircular.
Input Format
The first line contains a positive integer , the total number of houses. The next lines describe the positions of the houses. For , the -th house has coordinates given by a pair of integers and , separated by a space.
Output Format
Output a real number: the average number of houses covered by the antenna. The absolute error from the exact value must not exceed .
4
0 2
4 4
0 0
2 0
3.500
Hint
Sample note:
Any of 3.5, 3.50, 3.500, … is correct. In addition, 3.49, 3.51, 3.499999, … are also acceptable.
Constraints:
- For all , the coordinates are integers and . No three houses are collinear, and no four houses are cocircular.
- 40% of the testdata: .
- 70% of the testdata: .
- 100% of the testdata: .
Translated by ChatGPT 5

 京公网安备 11011102002149号
京公网安备 11011102002149号