Description

Ray 是某超大型实境节目的负责人。在节目开始不久，他就发现了有 $n_0$ 位参赛者非常擅长社交，这 $n_0$ 位参赛者已经和所有参赛者建立了关系。Ray 将这 $n_0$ 位参赛者称为「中心圈圈」，代号 $K_0$。

随着节目进展到中期，中心圈圈以外的参赛者们也逐渐形成了各自的「小圈圈」。Ray 观察到总共有 $t$ 个小圈圈，代号 $K_1, K_2, \ldots, K_t$，并且这些小圈圈分别有 $n_1, n_2, \ldots, n_t$ 位参赛者。每位参赛者只会恰好属于其中一个小圈圈或是中心圈圈。而 Ray 之所以把它称为小圈圈是因为对于所有属于小圈圈 $K_i$ $(1 \leq i \leq t)$ 的参赛者而言，他们只有和属于相同小圈圈 $K_i$ 以及中心圈圈 $K_0$ 的所有参赛者建立关系。

为了方便解释，下面会用图来表示这个实境节目，每个节点分别代表一位参赛者，而任两个节点之间有边代表这两位参赛者之间建立了关系，反之则没有。

举例来说，图(a)上有一个中心圈圈 $K_0$，两个小圈圈 $K_1$、$K_2$，$n_0=2$、$n_1=1$、$n_2=2$。假设中心圈圈的参赛者为 $\{\text{A}, \text{B}\}$，小圈圈的参赛者依序为 $\{\text{C}\}$、$\{\text{D}, \text{E}\}$，可以看到位于中心圈圈 $K_0$ 的参赛者和所有参赛者都有建立关系，相同小圈圈内的参赛者都有相互建立关系，并且对于分属不同小圈圈 $K_i$、$K_j$ $(1 \leq i < j \leq t)$ 的任两位参赛者而言，都没有建立关系。图(b)、(c)也是同样正确的范例。

:::align{center} :::

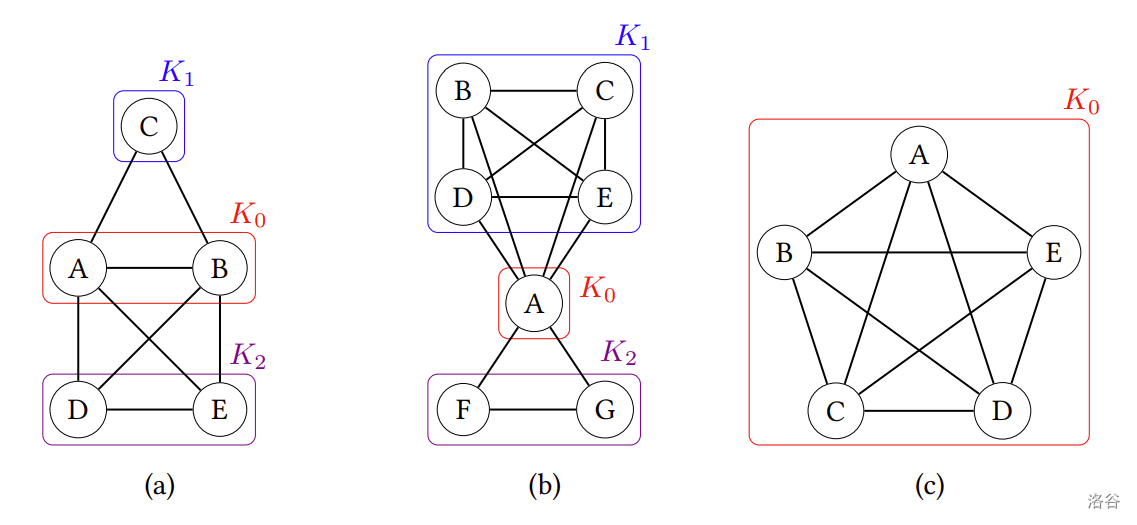而到了节目后期，Ray需要举办一场比赛，让所有建立了关系的任两位参赛者都进行一次对决，并且这些对决一定会有一方获胜。如果参赛者 $x$、$y$ 进行对决并且 $x$ 赢得胜利，则我们称 $x$ 比 $y$ 强；如果参赛者 $x$ 比 $y$ 强并且 $y$ 比 $z$ 强，则我们又称 $x$ 比 $z$ 强。

为了能够决定出最终赢家（可能有多个），Ray不希望存在三位参赛者 $x$、$y$、$z$ 使得 $x$ 比 $y$ 强，$y$ 比 $z$ 强，但 $z$ 又比 $x$ 强。

所以他需要先私下列出一份完整胜负关系，让所有参赛者照着这份胜负关系进行对决，使得最终结果满足他的要求。一份胜负关系若要被称为完整胜负关系，那对于任两位有建立关系的参赛者，都必须在胜负关系中决定出胜方是谁。

如果要用图来表示胜负关系，那么对于任两位有建立关系的参赛者 $x$、$y$，如果 $x$、$y$ 有进行对决，那就让 $x$、$y$ 之间的边指向胜方，例如 $x$ 赢得胜利就是指向 $x$。

举例来说，图(d)就是一份符合要求的完整胜负关系，最终赢家为 C 和 E。图(e)中的 B、E 有建立关系但没有分出胜负，所以它不是一份完整的胜负关系。而图(f)则是因为 A 比 C 强、C 比 B 强、但 B 又比 A 强，所以它没办法决定出最终赢家。

:::align{center} :::

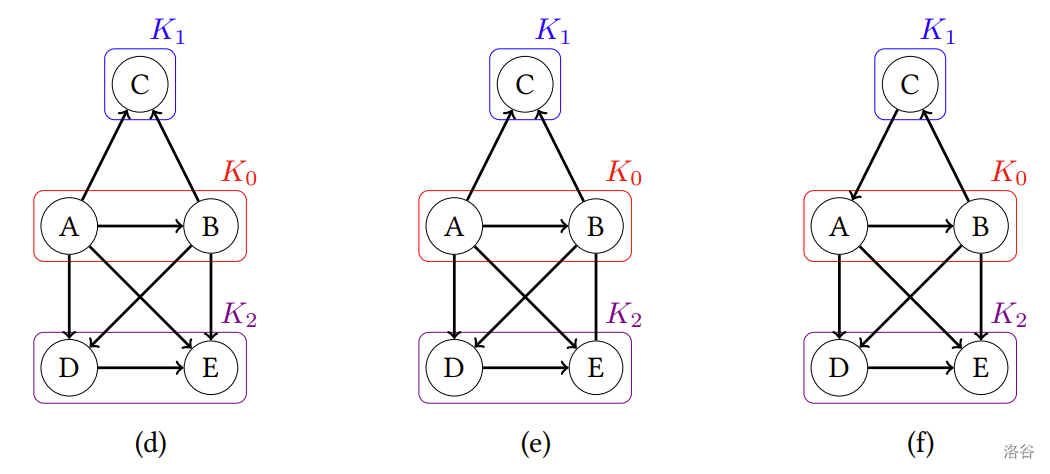Ray 想要知道对于给定的超大型实境节目，总共有几种符合要求的完整胜负关系。因为这个数字可能很大，你只要求出方法数除以 $10^9+7$ 的余数就行了。

Input Format

$$\begin{aligned} &t\\ &n_0 \ n_1 \ n_2 \ \ldots \ n_t \end{aligned}$$

• $t$ 代表小圈圈的数量。
• $n_0$ 代表属于中心圈圈的参赛者人数。
• $n_i$ 代表属于第 $i$ 个小圈圈 $K_i$ 的参赛者人数，$i \in \{1, 2, \ldots, t\}$。

Output Format

$$ans$$

• $ans$ 代表符合要求的完整胜负关系的数量 mod $10^9+7$ 后的结果。

2
2 1 2

72

3
5 7 6 9

6928820

Hint

数据限制

• $0 \leq t \leq 10^6$。
• $1 \leq n_i \leq 10^7$。
• 输入的数皆为整数。

评分说明

本题共有四组子任务，条件限制如下所示。 每一组可有一或多笔测试资料，该组所有测试资料皆需答对才会获得该组分数。

子任务	分数	额外输入限制
1	4	$t = 0$。
2	9	$t \leq 1$。
3	22	$t \leq 2$。
4	65	无额外限制。