Description

你是某出租车公司老板，拥有 $m$ 台出租车。这些出租车都在 $x$ 轴上，位置分别是 $t_1, t_2, t_3, \ldots,t_m$。同时，你接到 $m$ 名路人的搭车请求，这 $m$ 名路人也在 $x$ 轴上，位置分别是 $p_1, p_2, p_3, \ldots, p_m$。我们假设上述 $2m$ 个坐标均相异。你的任务是为每一位路人指派一台出租车，且每台出租车只能指派给一位路人。你的目标是最小化这 $m$ 台出租车到其指派路人的距离总和（称此距离总和为叫车距离总和）。你的程序必须输出最小叫车距离总和。

举例来说，如果你有 $2$ 台出租车（$m=2$），位置分别在 $100$ 与 $1$（$t_1=100, t_2=1$），而 $2$ 名路人位置分别在 $3$ 与 $101$（$p_1=3, p_2=101$），则最小叫车距离总和为 $|100-101|+|1-3|=3$。

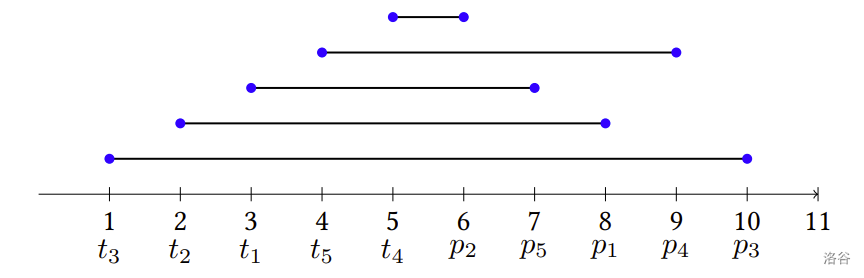
下图显示另一个例子。在这个例子中有 $5$ 台出租车（$m=5$），位置分别在 $3, 2, 1, 5, 4$（$t_1=3, t_2=2, t_3=1, t_4=5, t_5=4$），而 $5$ 名路人位置分别在 $8, 6, 10, 9, 7$（$p_1=8, p_2=6, p_3=10, p_4=9, p_5=7$），则最小叫车距离总和为 $25$（下图所显示的出租车指派方式之叫车距离总和即为 $25$）。

:::align{centered} :::

Input Format

$$\begin{aligned} &m \\ &t_1 \ t_2 \ \ldots \ t_m \\ &p_1 \ p_2 \ \ldots \ p_m \end{aligned}$$

• $m$ 代表路人及出租车的数量。
• $t_i$ 代表第 $i$ 辆出租车的位置。
• $p_i$ 代表第 $i$ 个路人的位置。

Output Format

$$a$$

• $a$ 代表给定输入的最小叫车距离总和。

5
3 2 1 5 4
8 6 10 9 7

25

5
10 70 30 90 50
71 31 51 91 11

5

Hint

数据限制

• $1 \leq m \leq 10^6$。
• $1 \leq t_i \leq 2 \times 10^6$。
• $1 \leq p_i \leq 2 \times 10^6$。
• 保证给定的 $2m$ 个坐标均相异。

评分说明

本题共有两组子任务，条件限制如下所示。 每一组可有一或多笔测试数据，该组所有测试数据皆需答对才会获得该组分数。

子任务	分数	额外输入限制
1	40	$\max_i\{t_i\} < \min_i\{p_i\}$。
2	60	无额外限制。