题目背景

翻译来自于 LibreOJ。

本题时限相较原时限翻倍。

题目描述

题目译自 Romanian Master of Informatics 2018 Day2 T2 「Squirrel」

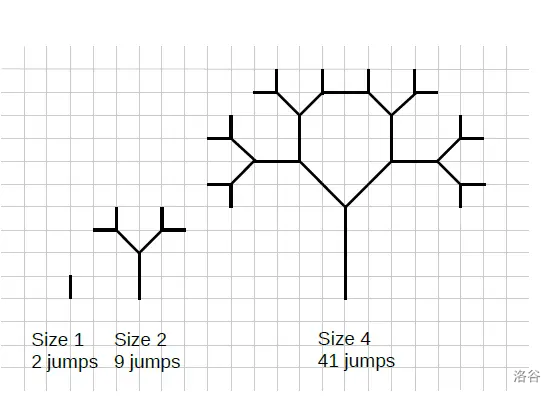
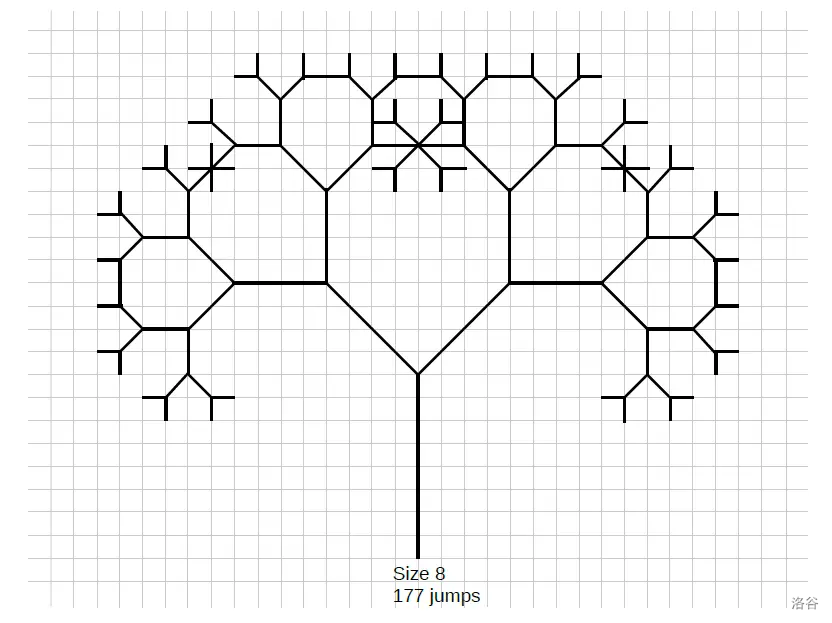
你站在一个 $M \times N$ 的树林网格的左上角，坐标为 $(1,1)$。一只松鼠在树间跳跃。作为一只计算机科学松鼠，它以特定的方式跳跃，形成了……树的分形图案！这些 $S$ 分形图案如图所示：

:::align{center} :::

:::align{center} :::

松鼠遵循以下规则：

• 松鼠从一棵指定的树开始跳跃。
• 它首先向北跳跃 $P$ 棵树，其中 $P$ 是给定的 $2$ 的幂。
• 然后，它沿两条长度为 $P/2$ 的对角线跳跃。
• 接着，它形成四个大小为 $P/2$ 的分形。
• 这一过程持续进行，直到创建出大小为 $1$ 的分形。
• 图中展示了大小为 $1$、$2$、$4$ 和 $8$ 的前四个分形。

松鼠会持续跳跃，直到完成一个分形图案，然后开始下一个分形。你想知道在多少棵树上可以看到这只松鼠？

输入格式

第一行包含三个整数 $M, N, F$，分别表示树林网格的行数、列数和分形数量。接下来的 $F$ 行描述 $F$ 个分形，每行包含三个整数，表示起始树的坐标以及分形大小。

输出格式

输出一个整数，表示可以看到松鼠的树的位置数量。

14 20 3
11 10 4
7 6 2
8 7 2

35

提示

样例 1 解释

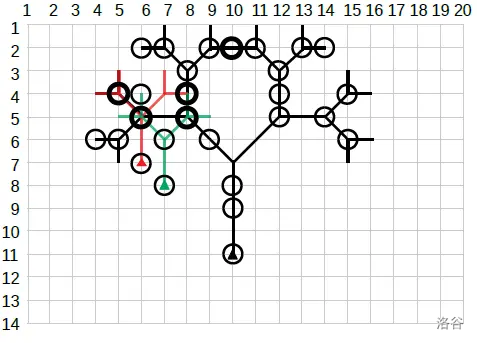
在样例中：

• 树林网格有 $14$ 行 $20$ 列。
• 松鼠跳跃三个分形，分别标记为黑色、红色和绿色。
• 三角形标记分形的起点。
• 圆圈标记从坐标 $(1, 1)$ 可见的树。
• 较粗的圆圈标记松鼠多次跳跃的可见树。
• 在可见树上的总跳跃次数为 $35$。

:::align{center} :::

数据范围

对于所有输入数据，满足：

• 如果你和松鼠所在树之间没有其他树阻挡，你可以看到松鼠。
• 松鼠完成当前分形的所有跳跃后停止，然后开始下一个分形。
• 松鼠永远不会跳到你的位置 $(1,1)$。
• 松鼠永远不会跳出树林网格。
• 如果松鼠多次跳到同一棵可见的树上，该树将多次计入最终结果。
• $2 \leq M, N \leq 50000$
• $1 \leq F \leq 1000$
• $1 \leq$ 分形大小 $\leq 1024$，分形大小为 $2$ 的幂
• 总跳跃次数最多为 $3\times 10^8$

每个测试点将单独评分。

子任务	分值	附加限制
$1$	$15$	总跳跃次数最多为 $4 \times 10^7$
$2$	$10$	总跳跃次数最多为 $6.5 \times 10^7$
$3$	$25$	总跳跃次数最多为 $1.25 \times 10^8$
$4$	$50$	无附加限制