题目背景

试题来源：https://loj.ac/p/2475，向 LOJ 和出题人表示感谢。如果版权方并不希望试题出现在洛谷，可联系洛谷管理组撤下试题。

题目描述

白云开始了一段旅程。

旅途中一共有 $n$ 个城市，编号为 $1$ 到 $n$，城市之间有一些道路相连。其道路结构可以抽象为一棵仙人掌。如果一个无向连通图的任意一条边最多属于一个简单环，我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。

:::align{center} :::

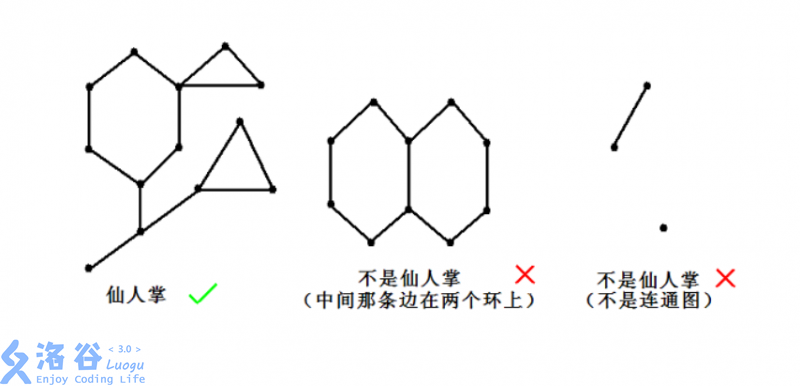白云对这些城市间的每条道路都有一个喜爱度。一条路径的喜爱度是其上所有道路的喜爱度的乘积。

现在白云在 $1$ 号城市准备出发。为了制定合理的路线，白云会时不时问白兔：“从 $1$ 号城市出发不经过重复道路到达 $k$ 号城市的所有路径喜爱度之和是多少？”

这可难倒了白兔，请你帮忙对于 $k=1,2,\ldots,n$ 求出相应答案。只需要输出答案对 $998244353( = 7\times 17\times 2^{23}+1$ 一个质数$)$取模后的值。

输入格式

第 $1$ 行两个正整数 $n,m$ 表示城市的个数和道路的条数。保证 $n \ge 2$。

接下来 $m$ 行每行两个正整数 $v,u,w(1 \le v,u \le n,1 \le w < 998244353)$ 表示一条连接城市 $v$ 和 $u$ 的喜爱度为 $w$ 的道路。

保证输入的图是一棵仙人掌，没有自环，但可能有重边。

输出格式

输出 $n$ 行，第 $i$ 行包含一个整数表示 $k=i$ 时的答案。

11 11
1 2 1
2 3 1
3 4 1
4 5 1
5 6 1
6 1 1
2 7 10
3 8 20
4 9 30
5 10 40
6 11 50

3
2
2
2
2
2
20
40
60
80
100

提示

注意，两条路径不同为它们经过的边数不同或存在一个满足 $1 \le x \le$ 路径长度 的 $x$ 使得这两条路径经过的第 $x$ 条边不同。

长度为 $0$ 的路径也是合法路径，权值视为 $1$。

对于所有数据，$n \le 10^5,1 \le w < 998244353$。

子任务编号	$n \leq$	$w \leq$	其它约定
$1$	$10^5$	$1$	$m=n-1$
$2$		$998244352$	^
$3$	$8$	^
$4$	$10^5$	$1$	一个点最多只在一个环中
$5$		$998244352$	^
$6$	$500$	^
$7$	$3000$	$1$	^
$8$		$998244352$
$9$	$10^5$	$1$
$10$		$998244352$

虽然我没有给 $m$ 的范围，但是熟悉仙人掌的小朋友都知道对于仙人掌肯定满足 $n-1 \le m \le 2n-2$。