Description

对于一棵树 $T=(V,E)$，$V$ 中每个点有一个互不相同的正整数标号。我们用点 $i$ 表示编号为 $i$ 的点。

定义这棵树的谷图为 $G(T)=(V,E')$。$G(T)$ 是无向简单图。存在边 $(u,v)\in E'$ 当且仅当在 $T$ 中，不存在一个异于 $u,v$ 的点 $x$ 满足 $x$ 在从 $u$ 到 $v$ 的简单路径上且其编号大于 $\min(u,v)$。

有一棵树 $T$，初始时只有一个点，编号为 $1$，接下来有 $q$ 次操作，操作有以下两种：

• $\texttt{1 u v}$ 表示加入一个编号为 $v$ 的节点并与当前编号为 $u$ 的节点相连（保证任何时刻不会有两个编号相同的节点）；
• $\texttt{2 u v}$ 表示查询 $G(T)$ 中点 $u$ 到 $v$ 的最短路（每条边长度均为 $1$）。

请你回答所有查询。

Input Format

第一行两个整数 $n, q$，表示编号的最大可能值及询问个数。

接下来 $q$ 行每行三个整数 $\texttt{op u v}$，以题目描述中的格式描述一次操作。

Output Format

依次对于每一个 $\texttt{2}$ 类型的操作，输出一行一个整数表示其对应的答案。

7 10
1 1 2
1 2 3
1 3 5
1 5 6
2 1 6
1 1 4
2 1 6
1 1 7
2 1 6
2 3 6

4
3
2
2

10 20
1 1 8
1 8 5
1 5 10
1 8 7
2 7 1
1 7 4
2 7 5
1 7 6
2 7 6
1 6 9
2 4 1
1 9 2
2 8 1
1 9 3
2 3 10
2 6 8
2 4 8
2 3 8
2 3 9
2 8 1

2
2
1
3
1
2
2
2
2
1
1

10 20
1 1 7
1 7 6
1 1 2
1 6 4
1 2 3
1 3 5
1 5 9
1 9 8
1 8 10
2 7 10
2 8 3
2 9 5
2 1 7
2 2 1
2 9 9
2 2 7
2 4 3
2 5 4
2 9 2
2 1 1

2
3
1
1
1
0
1
3
3
2
0

Hint

样例 1 解释

最终的树 $T$ 和 $G(T)$ 如下：

:::align{center} :::

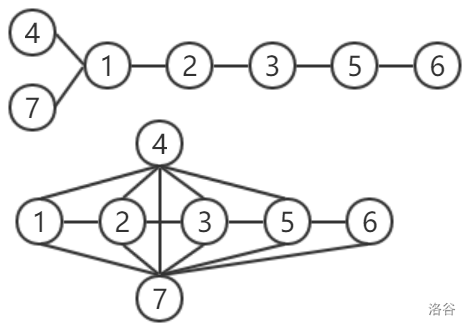第一次询问的路径：$1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6$；

第二次询问的路径：$1 \rightarrow 4 \rightarrow 5 \rightarrow 6$；

第三次询问的路径：$1 \rightarrow 7 \rightarrow 6$；

第四次询问的路径：$3 \rightarrow 5 \rightarrow 6$。

数据范围与提示

对于所有数据，$1\le n\le 10^5,1\le q\le 5\times 10^5$。

每个子任务详细的数据限制及约定如下（留空表示和上述所有数据的约定相同）：

性质一：所有 $\texttt{1}$ 操作（修改）在所有 $\texttt{2}$ 操作（询问）之前。

性质二：任何时刻保证树是一条链。

性质三：最终形成的树在所有 $n$ 个点的有标号无根树中均匀随机，随机数生成器使用梅森旋转算法。

注意样例 3 满足性质一、二。