Description

In a 2D coordinate system, there are $n$ platforms (a platform is defined as a horizontal open line segment whose two endpoints share the same $y$-coordinate; an open line segment means its two endpoints are not part of the segment itself) and one iron ball. If there is no object directly below, the ball falls $1$ unit length per second.

Each time the ball lands on a platform, the player may choose to roll horizontally to the left or to the right. The rolling speed is $1$ unit length per second. Because the iron ball is fragile, the height of each single drop must not exceed $h$.

Design a strategy to make the ball reach the ground as quickly as possible without breaking.

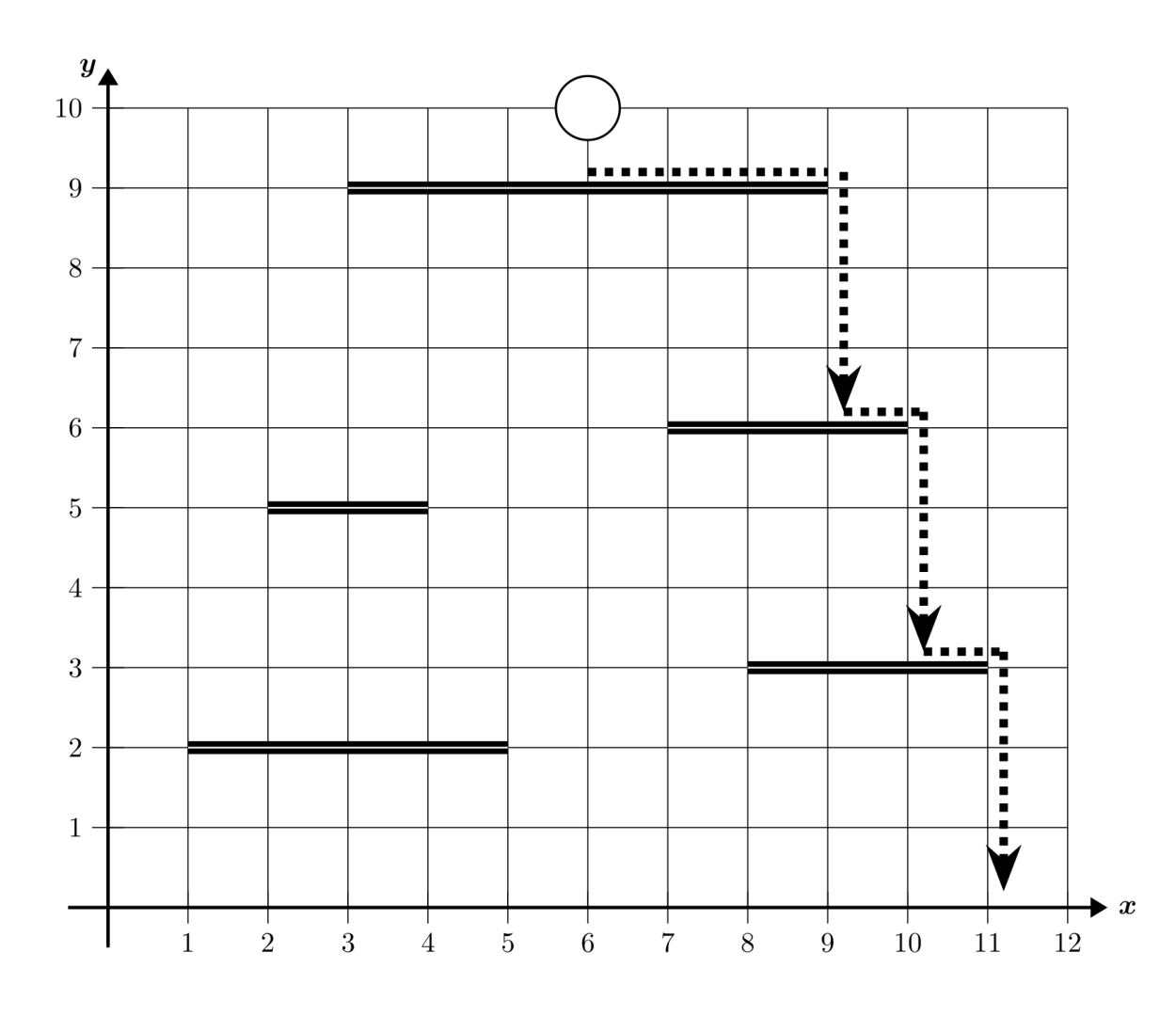
Assume the ground has height $0$ and is infinitely wide. The ball’s size is negligible compared to the platforms and can be treated as a point mass. Please note: the ball begins to fall as soon as it reaches an endpoint of a platform; it does not need to roll into the next cell. For example, in the figure below, the ball at $(9, 9)$ has already started to fall.

Input Format

The first line contains two integers representing the number of platforms $n$ and the maximum allowed drop height $h$.

The second line contains two integers $x, y$, indicating that the iron ball starts at position $(x, y)$.

Lines $3$ to $n + 2$: each line contains three integers. On line $i + 2$, the integers $h_i, l_i, r_i$ denote the $y$-coordinate $h_i$ of the $i$-th platform and the $x$-coordinates $l_i, r_i$ of its left and right endpoints, respectively.

Output Format

Output one line with a single integer: the minimum total time to reach the ground.

5 3
6 10
5 2 4
9 3 9
6 7 10
2 1 5
3 8 11

15

10 156
84 139
63 22 50
79 96 100
87 77 98
60 24 53
47 1 29
62 55 89
68 68 78
10 5 85
85 67 71
73 57 61

155

Hint

Constraints and Conventions

For all test points, it is guaranteed that:

• $1 \leq n \leq 10^5$.
• $1 \leq x, y, h, h_i, l_i, r_i \leq 10^9$, $l_i \leq r_i$.
• All $h_i$ are pairwise distinct; all $l_i$ and $r_i$ are also pairwise distinct; and for any $i \neq j$, it holds that $l_i \neq r_j$.
• The testdata guarantees there is a solution, and the final answer does not exceed $10^9$.

Translated by ChatGPT 5