#P13011. 【MX-X13-T6】「KDOI-12」能做到的也只不过是静等缘分耗尽的那一天。
【MX-X13-T6】「KDOI-12」能做到的也只不过是静等缘分耗尽的那一天。
Description
For a permutation , construct its max-heap Cartesian tree, then disconnect the edge between each node and its right child (if it exists). Denote the resulting forest as .
For example, consider . The max-heap Cartesian tree and are shown below:
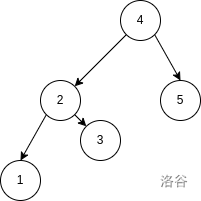
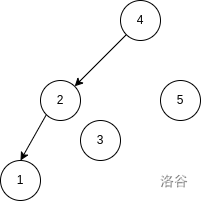
Given , you need to determine how many of the permutations of satisfy that nodes and belong to the same tree in . Nodes are identified by their indices, not their values in .
Since the answer may be large, output it modulo a prime .
Input Format
This problem contains multiple test cases.
The first line contains two positive integers and , representing the number of test cases and the modulo. It is guaranteed that is a prime. For each test case:
- One line with three positive integers .
Output Format
For each test case, output a non-negative integer indicating the number of valid permutations modulo .
10 1000000007
4 1 4
4 2 2
4 3 2
5 4 2
7 3 5
8 2 7
10 3 8
100 99 6
1000 234 789
5000 1234 4321
6
24
8
25
882
3840
270000
220955222
251832899
768412458
Hint
Sample Explanation
For the first test case, the following permutations satisfy the condition:
$[1, 2, 3, 4], [1, 3, 2, 4], [2, 1, 3, 4], [2, 3, 1, 4], [3, 1, 2, 4], [3, 2, 1, 4]$.
For the second test case, all permutations are valid.
Constraints
This problem uses bundling tests.
| Subtask | Points | Special Constraints | ||
|---|---|---|---|---|
| None | ||||
| A | ||||
| None |
- Special Constraint A: .
For all test cases:
- ,
- ,
- and is a prime.
Hint
Please use a fast input method.
Translation by DeepSeek V3.

 京公网安备 11011102002149号
京公网安备 11011102002149号