Description

你正在开发一款游戏，玩家将在二维地图中驾驶汽车收集道具。

地图上有 $N$ 个可以获取道具的箱子。第 $i$ 个箱子的位置是 $(x_i, y_i)$，每当汽车经过这个位置时，可以获得 $w_i$ 个道具。

汽车只能沿与 x 轴或 y 轴平行的方向移动。汽车的每次移动通过两个整数 $d$ 和 $v$ 来表示：

• 若 $d = 0$，表示 x 坐标增加 $v$；
• 若 $d = 1$，表示 y 坐标增加 $v$；
• 若 $d = 2$，表示 x 坐标减少 $v$；
• 若 $d = 3$，表示 y 坐标减少 $v$。

此时，位于起点位置的箱子不能获取道具。换句话说，如果汽车从 $(s_x, s_y)$ 移动到 $(e_x, e_y)$，则不能获取 $(s_x, s_y)$ 位置的箱子的道具，但可以获取 $(e_x, e_y)$ 位置的箱子的道具。

汽车从 $(1, 1)$ 开始，接下来会移动 $Q$ 次。给出汽车的移动方向和距离，计算 $Q$ 次移动过程中能够获得的道具总数。

Input Format

第一行包含两个用空格分隔的整数 $N$ 和 $Q$，分别表示箱子的数量和汽车的移动次数。

接下来的 $N$ 行中，每行包含三个整数 $x_i$、$y_i$、$w_i$，表示第 $i$ 个箱子的位置在 $(x_i, y_i)$，且经过该位置可以获得 $w_i$ 个道具。

接下来的 $Q$ 行中，每行包含两个整数 $d_j$、$v_j$，表示汽车向方向 $d_j$ 移动距离 $v_j$。

Output Format

输出一行，表示 $Q$ 次移动过程中能获得的道具总数。

4 6
5 5 3
5 8 5
3 5 2
1 5 1
0 4
1 9
3 5
2 3
2 1
0 5

24

3 3
1 3 1
2 2 1
3 1 1
1 3
0 2
3 3

2

Hint

样例 1 说明

如图所示，每次移动都会获得绿色标记的物品。

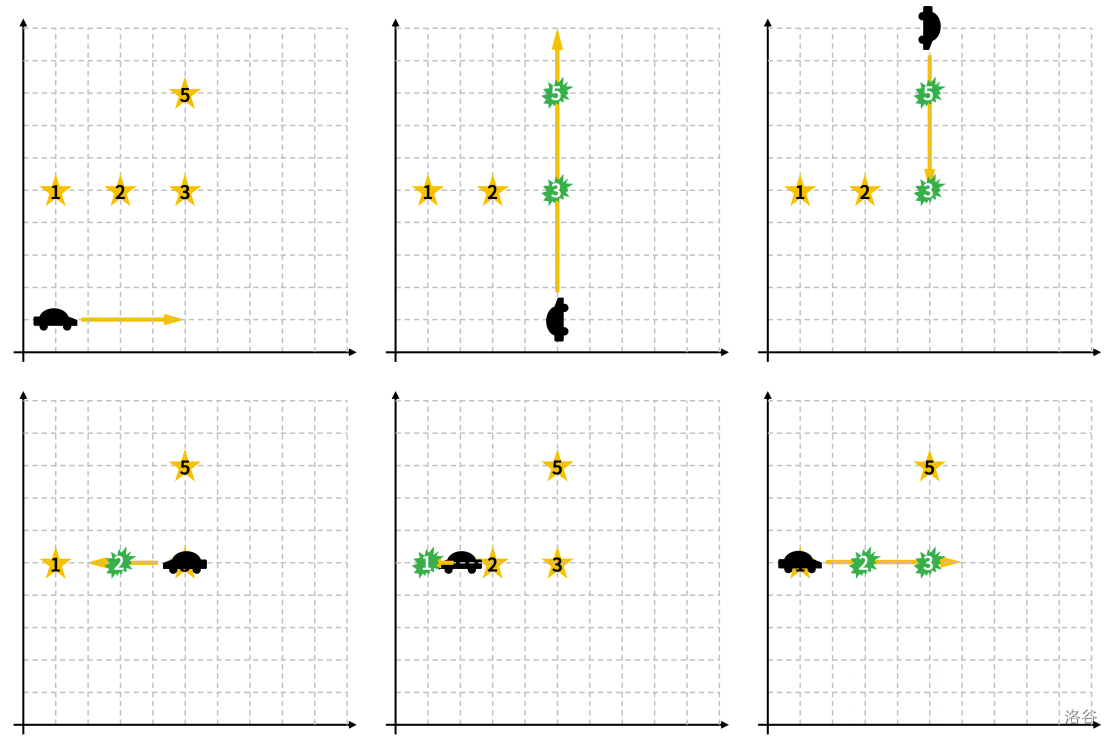
限制条件

• 所有输入数值均为整数。
• $1 \leq N \leq 200\,000$
• $1 \leq Q \leq 200\,000$
• $1 \leq x_i \leq 200\,000$
• $1 \leq y_i \leq 200\,000$
• $1 \leq w_i \leq 200\,000$
• $0 \leq d_j \leq 3$
• $1 \leq v_j \leq 200\,000$
• 所有箱子的位置彼此不同。
• 汽车在任意时刻的 x、y 坐标都在 $[1, 200\,000]$ 范围内。

子问题

1. （9 分）$N \leq 2\,000$，$Q \leq 2\,000$，$x_i \leq 1\,000$，$y_i \leq 1\,000$，$w_i \leq 10$，汽车所有时刻的坐标 $\leq 1\,000$
2. （17 分）$N \leq 2\,000$，$Q \leq 2\,000$，$w_i \leq 10$
3. （15 分）所有箱子的 x 坐标互不相同，且 y 坐标也互不相同。
4. （37 分）所有 $w_i = 1$
5. （22 分）无额外限制。

翻译由 ChatGPT-4o 完成