Description

Given a rooted tree with $n$ nodes (numbered $1$ to $n$, root is node $1$).

Each node $i$ has a pair $(dep_i, str_i)$ where:

• $dep_i$ is the distance from $i$ to the root.
• $str_i$ is the string formed by concatenating the IDs of all nodes along the simple path from the root to $i$ (the character set consists of node IDs).

There are $q$ queries. For each query $(x, k)$, compute $f(x, k)$ as follows:

1. Find the set $S$ of node IDs in the $(x, k)$-neighborhood.
2. Sort $S$ in ascending order by their pairs (using $dep$ as the primary key and $str$'s lexicographical order as the secondary key). Let the sorted list be $c_1, c_2, \ldots, c_{|S|}$.
3. $f(x, k)$ is defined as $\sum_{i=1}^{|S|-1} \operatorname{Dis}(c_i, c_{i+1})$.

Definitions:

• $\operatorname{Dis}(u, v)$: The number of edges on the unique simple path between $u$ and $v$.
• $(u, d)$-neighborhood: The set of nodes whose distance from $u$ is $\le d$.

Input Format

• First line: Two integers $n, q$ (number of nodes and queries).
• Second line: $n-1$ integers where the $i$-th integer is the parent $p_{i+1}$ of node $i+1$.
• Next $q$ lines: Two integers $x, k$ per line (query parameters).

Output Format

Output $q$ lines, each containing the answer to the corresponding query.

10 3
1 2 2 3 4 5 6 6 9 
1 3
3 2
4 3

11
8
15

10 10
1 2 2 3 4 5 6 6 9 
1 3
3 2
4 3
10 3
2 2
3 3
5 3
1 0
7 2
1 2

11
8
15
5
11
16
8
0
2
4

Hint

Explanation #1

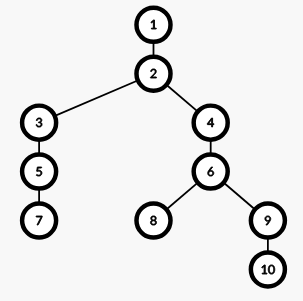
The pairs for each node are (where "|" is used only to separate characters in strings):

For query $(1, 3)$:

• $c$ sequence: $1,2,3,4,5,6$
• $f(1,3) = \operatorname{Dis}(1,2)+\operatorname{Dis}(2,3)+\operatorname{Dis}(3,4)+\operatorname{Dis}(4,5)+\operatorname{Dis}(5,6) = 11$.

For query $(3, 2)$:

• $c$ sequence: $1,2,3,4,5,7$
• $f(3,2) = 8$.

For query $(4, 3)$:

• $c$ sequence: $1,2,3,4,5,6,8,9,10$
• $f(4,3) = 15$.

Constraints

This problem uses subtask scoring.

For all test data: $1 \le n, q \le 5 \times 10^5$, $1 \le p_i < i$, $1 \le x \le n$, $0 \le k \le n$.

• Special Property A: Parent nodes are randomly generated within valid ranges.
• Special Property B: All leaf nodes have the same depth.

Note: Use fast I/O methods for this problem.

Translated by DeepSeek R1