Description

在二维平面上，有 $N$ 根柱子按顺序排列。柱子从左到右编号为 $1$ 到 $N$。第 $i (1 \leq i \leq N)$ 根柱子的底部位于点 $(D_{i}, 0)$，高度为 $H_{i}$。因此，这根柱子是连接点 $(D_{i}, 0)$ 和 $(D_{i}, H_{i})$ 的线段。此外，$D_{1}=0$。

一开始，松鼠位于最左边柱子的高度为 $L$ 的位置，即点 $(0, L)$。松鼠需要依次经过所有柱子，最终到达最右边柱子的高度为 $R$ 的位置，即点 $(D_{N}, R)$。

当松鼠从一根柱子飞到下一根柱子时，如果向右移动 $d (d \geq 0)$，高度会下降 $d$。在到达下一根柱子之前，松鼠不能碰到地面。到达下一根柱子的高度为 $0$ 的位置是允许的。

松鼠可以在一根柱子上向上爬或向下滑，但不能爬到超过柱子高度的位置。在第 $i$ 根柱子上向上爬 $h (h \geq 0)$ 需要花费 $W_{i} \times h$ 的费用。向下滑动不需要费用。

下图是飞天松鼠移动的一个例子。

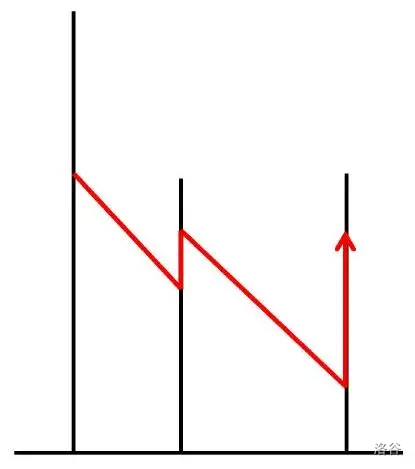
下图左侧的移动方式由于中途碰到地面，因此不允许。下图右侧的移动方式由于没有经过所有柱子，也不允许。

请计算松鼠以最小总费用到达目标位置的方法。

你需要实现以下函数：

long long fly(vector<int> D, vector<int> H, vector<int> W, int L, int R);

• 该函数只会被调用一次。
• 给定的三个数组的大小为柱子的数量 $N$。
• 给定的整数数组 $D$ 中，$D[i]$ 表示第 $1$ 根柱子到第 $i+1$ 根柱子的距离 $D_{i+1}$。
• 给定的整数数组 $H$ 中，$H[i]$ 表示第 $i+1$ 根柱子的高度 $H_{i+1}$。
• 给定的整数数组 $W$ 中，$W[i]$ 表示第 $i+1$ 根柱子上每上升 $1$ 单位距离的费用 $W_{i+1}$。
• 给定的整数 $L$ 表示飞天松鼠在第 $1$ 根柱子上的初始高度。
• 给定的整数 $R$ 表示飞天松鼠在第 $N$ 根柱子上需要到达的高度。

该函数的返回值应为：

• 如果有方法遵守规则到达最终位置，返回飞天松鼠到达最终位置的最小费用。可以证明，满足约束条件的输入数据的最小费用总是整数。
• 如果没有方法遵守规则到达最终位置，返回 -1。

注意，提交的代码中不应包含任何输入输出操作。

Input Format

示例评测程序按以下格式读取输入：

• 第 $1$ 行：$N$
• 第 $1+i (1 \leq i \leq N)$ 行：$D_{i}\,H_{i}\,W_{i}$
• 第 $2+N$ 行：$L\,R$

Output Format

示例评测程序按以下格式输出：

第 $1$ 行：函数 fly 返回的值。

3
0 8 3
2 5 4
5 5 6
5 4

18

3
0 4 6
3 2 5
5 6 3
1 5

37

Hint

样例解释 #1

考虑 $N=3$，第 $1$ 根柱子到第 $2$ 根柱子的距离为 $2$，第 $1$ 根柱子到第 $3$ 根柱子的距离为 $5$，柱子的高度从左到右分别为 $8,5,5$，柱子的权重从左到右分别为 $3,4,6$，$L=5, R=4$ 的情况。

评测程序将调用如下函数：

fly([0,2,5],[8,5,5],[3,4,6], 5,4)=18

在这种情况下，从第 $1$ 根柱子上升 $2$ 个单位距离，然后在第 $3$ 根柱子上升 $2$ 个单位距离是最优的，因此函数应返回 $18$。

这个例子满足子任务 $3,4,5,6$ 的条件。

数据范围

对于所有输入数据，满足：

• $2 \leq N \leq 5\cdot 10^5$
• $0=D_{1}<D_{2}<\cdots<D_{N} \leq 10^{9}$
• $1 \leq H_{i} \leq 10^{9}(1 \leq i \leq N)$
• $0 \leq W_{i} \leq 10^{9}(1 \leq i \leq N)$
• $0 \leq L \leq H_{1}$
• $0 \leq R \leq H_{N}$

详细子任务附加限制及分值如下表所示。