Description

Given $n$ matchsticks, how many equations of the form $A+B=C$ can you make? In the equation, $A$, $B$, and $C$ are integers formed with matchsticks (if the number is nonzero, its most significant digit cannot be $0$). The ways to form the digits $0$ to $9$ with matchsticks are shown in the figure:

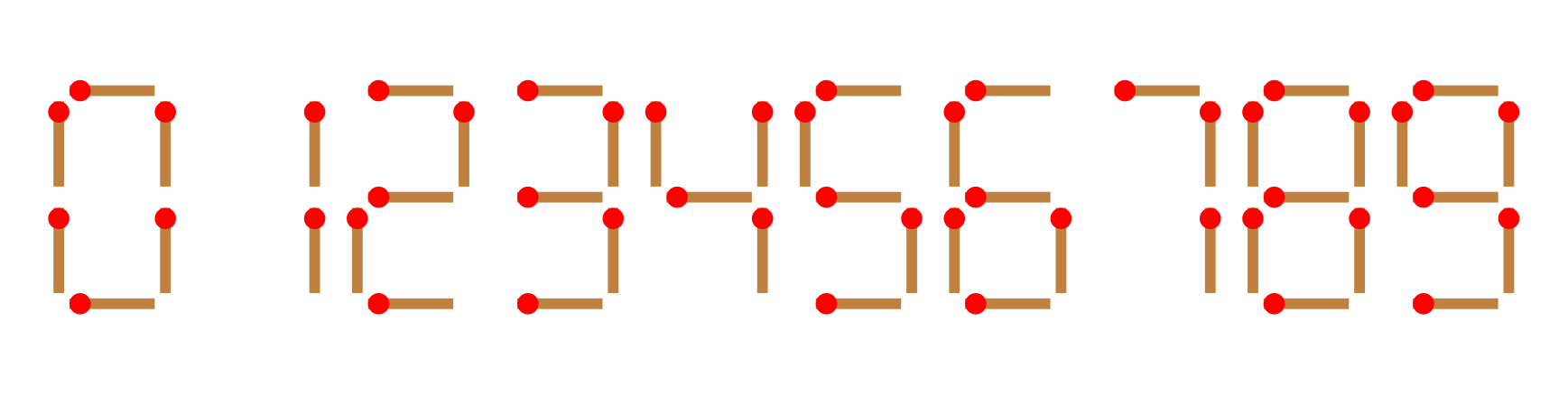
Note:

1. The plus sign and the equals sign each require two matchsticks.
2. If $A\neq B$, then $A+B=C$ and $B+A=C$ are considered different equations ($A,B,C\geq 0$).
3. All $n$ matchsticks must be used.

Input Format

A single integer $n$ ($1 \leq n \leq 24$).

Output Format

A single integer, the number of different equations that can be formed.

14

2

18

9

Hint

[Explanation for Sample 1]

The $2$ equations are $0+1=1$ and $1+0=1$.

[Explanation for Sample 2]

The $9$ equations are $0+4=4$, $0+11=11$, $1+10=11$, $2+2=4$, $2+7=9$, $4+0=4$, $7+2=9$, $10+1=11$, $11+0=11$.

NOIP 2008 Senior Problem 2.

Translated by ChatGPT 5