Description
考古学家们决定统计一个算法在 ROI 中考察的次数。为此,他们构建了一个由小写英文字母组成的字符串 p,并希望找出这个字符串在解压缩后的字符串 t 中的出现次数。
如果长度为 m 的字符串 p 作为子串从位置 i 开始出现,那么从第 i 个字符开始的连续 m 个字符串将是字符串 p。例如,字符串 aba 在字符串 ababaaba 中作为子串出现三次,分别从第 1,3,6 个字符开始。
请编写一个程序,确定给定字符串 p 在解压缩后的字符串 t 中出现的次数。
第一行包含两个自然数 m 和 n,分别表示字符串 p 的长度和压缩文本中的块数。
第二行包含一个非空字符串 p,由小写英文字母组成。
接下来的 n 行,包含按照题目背景的格式给出的块的描述。
输出一个整数,表示字符串 p 在文本中出现的次数。
3 4
aba
1 ab
2 1 3
2 3 3
2 1 8
6
Hint
样例解释:
t 的解压缩过程是这样的:
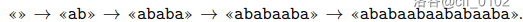
aba 在 ababaabaababaaba 中出现了 6 次。
数据范围:
设将前 i 块解压缩后字符串的长度为 Li,第 i 块的类型为 typei。
| 子任务 |
分值 |
m≤ |
n≤ |
Ln≤ |
其它特殊性质 |
| 1 |
6 |
2000 |
1 |
1000 |
|
| 2 |
10 |
105 |
2000 |
106 |
| 3 |
2000 |
1010 |
∀i>1,typei=2,posi=1,L1∣leni |
| 4 |
posi=Li−1 |
| 5 |
20 |
posi=1,leni≤107 |
| 6 |
4 |
2000 |
| 7 |
10 |
20 |
p 只含字母 a,posi+leni−1≤Li−1 |
| 8 |
6 |
posi+leni−1≤Li−1 |
| 9 |
2 |
1 |
2000 |
p 只含字母 a |
| 10 |
4 |
20 |
| 11 |
5 |
|
| 12 |
14 |
105 |
| 13 |
9 |
2×105 |
10000 |
1015 |
对于 100% 的数据,∑w≤2×105。

 京公网安备 11011102002149号
京公网安备 11011102002149号