题目背景

题目来源：https://hsin.hr/hio2023/。翻译来自 文心一言。如果有更好的翻译请在讨论区提供。

题目描述

夜幕降临，必须小心行事。在玛格丽塔成功地与所有客人打招呼之后，他们无阻碍地坐在了长椅上。

我们可以用从 $1$ 到 $N$ 的数字来标记客人，正好是他们坐在长椅上的顺序。由于未知的原因，在索托尼举办的盛大舞会上，客人的数量总是 $2$ 的幂次。然而，玛格丽塔现在遇到了问题，因为每对客人之间都存在着一定程度的不耐烦，我们可以用一个非负数字来表示这种不耐烦。客人之间的不耐烦可以标记为 $netrp(i, j)$。始终有 $netrp(i, j) = netrp(j, i)$，并且 $netrp(i, i) = 0$。由于客人们已经（不）舒适地就座，玛格丽塔不能突然改变他们的顺序。实际上，客人们也不知道自己处于完全二叉树（velikog Sotoninog potpunog binarnog stabla，VSPBS）的列表中，这在图片中以 $N=4$ 的情况展示了出来。

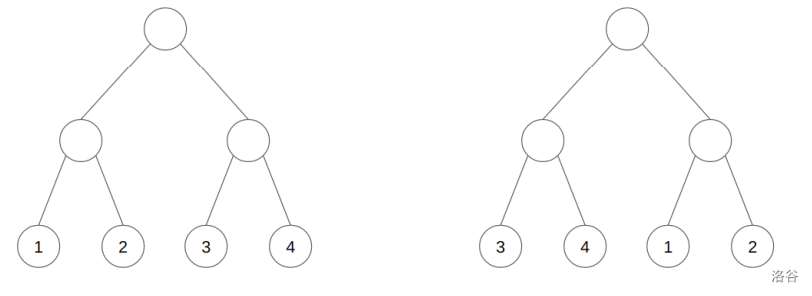
(a) 图 1：初始的树结构，(b) 图 2：操作后的树结构

玛格丽塔可以选择一个节点，并在一次操作中交换该节点的左孩子和右孩子，从而改变位于相应叶子节点上客人的顺序。展示的是树结构（以及长椅上的状态），在玛格丽塔对树的根节点进行一次操作之后的状态。玛格丽塔可以对任意节点进行任意次数的操作。长椅上的总不耐烦度定义为长椅上所有相邻客人之间的不耐烦度之和。帮助玛格丽塔确定她可以达到的最小可能的长椅不耐烦度。

输入格式

在第一行是一个自然数 $N$，表示客人数量。在接下来的 $N$ 行中，第 $i$ 行包含按顺序排列的数字 $netrp(i, j)$，这些数字满足上述属性。

输出格式

输出最小的不耐烦度。

2
0 2
2 0

2

4
0 2 3 1
2 0 4 5
3 4 0 3
1 5 3 0

6

8
0 2 5 8 5 9 2 6
2 0 8 4 3 7 5 3
5 8 0 3 8 4 3 3
8 4 3 0 2 2 7 7
5 3 8 2 0 7 3 3
9 7 4 2 7 0 6 7
2 5 3 7 3 6 0 4
6 3 3 7 3 7 4 0

25

提示

【样例解释】

在第二个例子中，一个可能的排列方式可以达到最小不耐受度的是 $2,1,4,3$。

【数据范围】

在所有子任务中，都满足 $1 \leq N \leq 2048$，且 $N$ 是 $2$ 的幂次，$0 \leq netrp(i,j) \leq 10^9$。

• 子任务 1（10 分）：$N\leq 16$；
• 子任务 2（17 分）：$N\leq 128$；
• 子任务 3（32 分）：$N\leq 512$；
• 子任务 4（41 分）：无特殊限制；