#P10678. 『STA - R6』月
『STA - R6』月
Description
For a tree with nodes, its diameter is defined as the maximum distance between any two nodes.
Given a positive integer and the degree of each node , construct a tree that minimizes . It is guaranteed that at least one valid tree exists. If multiple valid answers exist, output any one of them.
Input Format
This problem contains multiple test cases within a single test point.
The first line contains a positive integer , representing the number of test cases.
For each test case:
- The first line contains a positive integer .
- The second line contains positive integers, where the -th integer denotes the degree of node .
Output Format
For each test case, output lines. Each line contains two positive integers and , representing the edges of the constructed tree.
4
2
1 1
3
1 1 2
5
1 1 2 2 2
7
1 3 2 3 1 1 1
2 1
1 3
3 2
5 4
4 2
3 1
3 5
4 2
3 2
1 2
5 4
6 4
7 3
Hint
Sample Explanation
For the last test case in the sample input, the constructed tree is shown below:
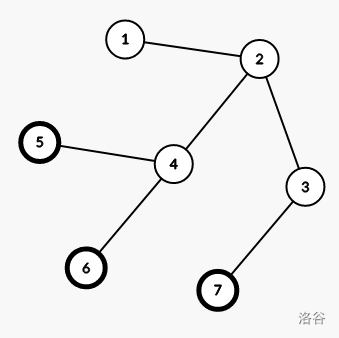
Its diameter equals the distance between nodes and or nodes and , which is . It can be proven that no tree satisfying the conditions has a diameter smaller than .
Data Constraints
This problem uses subtask scoring.
For of the data:
- ;
- ;
- ;
- ;
- It is guaranteed that at least one valid solution exists.
Detailed subtask allocations are as follows:
| Subtask ID | Data Range | Points |
|---|---|---|
| 1 | 17 | |
| 2 | 23 | |
| 3 | contains only two distinct values | 26 |
| 4 | No additional constraints | 34 |
Translation by DeepSeek R1

 京公网安备 11011102002149号
京公网安备 11011102002149号