#P10605. 下头论文
下头论文
Description
One day, Renko discovered an excellent idea and wanted to refine it through experiments. Specifically, she needs to complete tasks sequentially, where the -th task requires consecutive days to complete. This means if she starts the task on day , she will finish it after day . She must ensure she is free on all those days.
Unfortunately, she has days with prior commitments, given as a monotonically increasing sequence . That is, for any (), .
Renko wants to minimize the total time taken to complete all tasks. For example: suppose she needs to complete 2 tasks, where the first takes 2 days and the second 3 days, and she has a commitment on day 4. The figure below shows a scenario where Renko finishes all tasks in the shortest possible time of 7 days:
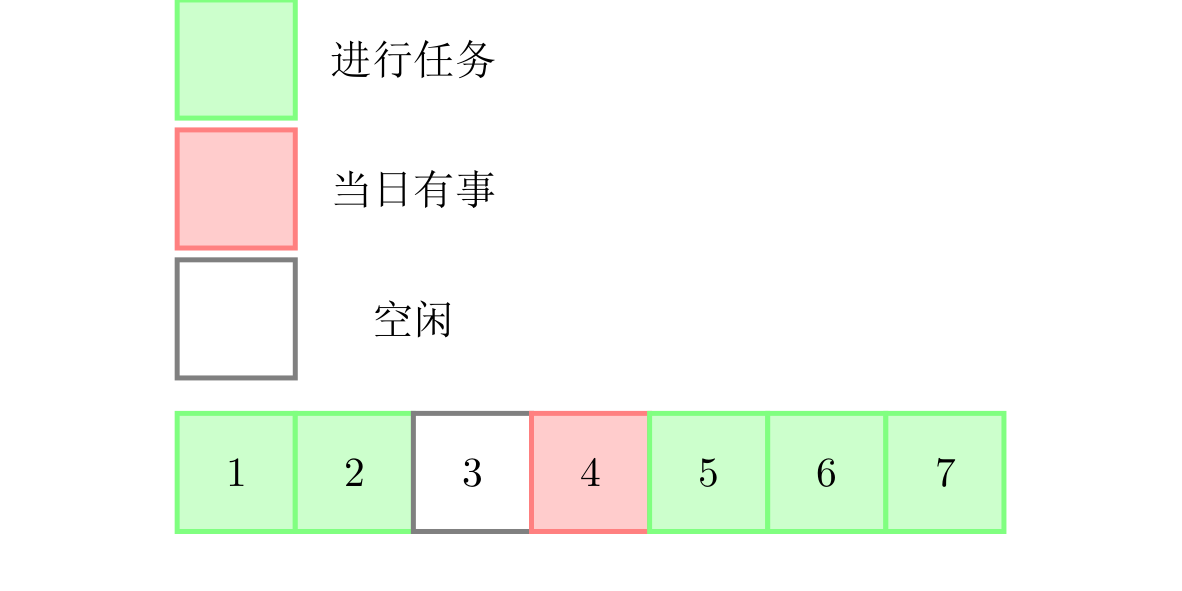
- Green: be in progress
- Red: be busy
- Blank: spare time
She wants to determine the earliest day she can complete all tasks under optimal conditions.
Input Format
- The first line contains two integers and .
- The second line contains positive integers describing sequence .
- The third line contains positive integers describing sequence , which is guaranteed to be monotonically increasing.
Output Format
Output one integer: the earliest day Renko can finish all tasks.
2 1
2 3
4
7
3 3
1 1 1
1 5 6
4
Hint
Sample #1
This matches the scenario described in the problem. Renko starts the first task on day 1 and finishes it after day 2. Due to her commitment on day 4, she cannot start the second task on day 3. Instead, she starts it on day 5 and completes it after day 7.
This sample satisfies the special property of Subtask 2.
Sample #2
Renko completes all tasks consecutively from day 2 to day 4.
Constraints
Bundled testing is used. All test cases in a Subtask must be passed to receive its points.
Note: denotes the sum of all (i.e., ). The same applies to other problems unless stated otherwise.
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{Points} & \bm{n,m \leq} & \bm{\sum a_i \leq} & \bm{b_i \leq} & \textbf{Special Property} & \textbf{Subtask Dependencies} \cr\hline 1 & 20 & 10 & 100 & 100 & - & - \cr\hline 2 & 20 & 10^5 & 10^8 & 10^8 & m=1 & - \cr\hline 3 & 20 & 10^3 & 10^8 & 10^8 & \text{None} & - \cr\hline 4 & 40 & 10^5 & 10^8 & 10^8 & \text{None} & 1,2,3 \cr\hline \end{array}$$For all data: , , , and is monotonically increasing.
Translated by DeepSeek R1

 京公网安备 11011102002149号
京公网安备 11011102002149号