Description

现在我们将在树上进行简化版的生命游戏，首先将给出一棵含有 $n$ 个点，$n-1$ 条边的树和一个整数 $k$。

在每回合时，当前剩余的度数为 $k$ 的点及与其连接的边会瞬间同时被删去。

形式化的，每回合都将按顺序进行如下操作：

• 统计当前剩余每个点的度数（一个点的度数定义为为，这个点当前连接的边的条数）。
• 将所有度数恰好为 $k$ 的点标记。
• 将上一步标记的点及其连接的边全部删去。

我们希望知道在无穷多回合后，这棵树将被分为多少个连通块。若最终两个点能够直接或间接的通过若干条边相连，则认为这两个点属于同一个连通块。

Input Format

第一行两个整数 $n,k$ ($0\le k < n \le 10^6$)，用空格隔开。

接下来 $n-1$ 行，每行两个用空格隔开的正整数 $u_i,v_i$ ($1\le u_i, v_i \le n$) 表示 $u_i$ 和 $v_i$ 之间有一条边。

输入的数据量较大，建议使用快速的读入方式。

Output Format

共一行一个整数，表示无穷多回合之后剩余的连通块个数。

3 1
1 2
2 3

1

4 2
1 2
2 3
3 4

2

10 3
1 2
2 3
9 4
3 5
5 6
6 7
3 9
5 8
5 10

5

Hint

对于样例 1:

这棵树的初始形态为：

其中三个点的度数依次为 $1,2,1$。

在一回合过后，点 $1,3$ 被删除。

这棵树变为：

容易发现之后这棵树的形态将不会变化，所以最终的连通块个数是 $1$。

对于样例 2：

初始形态为：

一回合之后变为：

之后保持不变，最终连通块个数为 $2$。

对于样例 3：

初始形态：

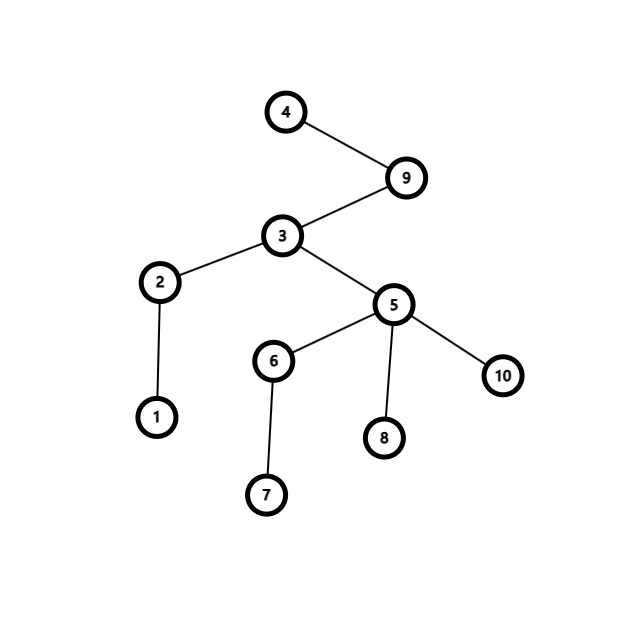
一回合之后变为：

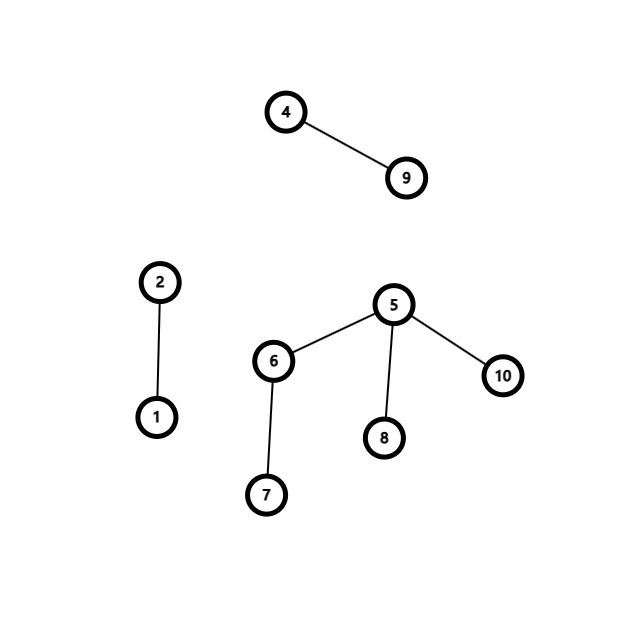
再过一回合之后变为：

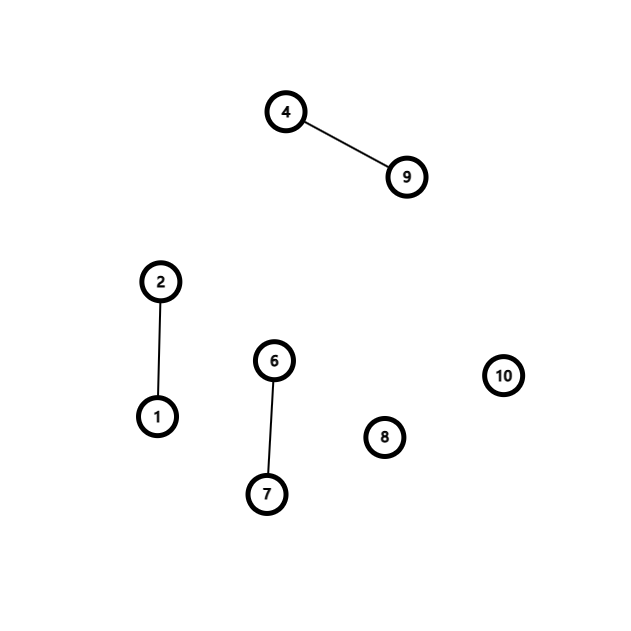
之后保持不变，最终连通块个数为 $5$。