Description
白色光可以被分解成青色光还有很多其他颜色的光。
{a} 是一个长度为 n,有 k 种不同颜色的序列,第 i 个元素颜色为 ai(保证颜色 1∼k 都在 a 中出现过)。
{b} 是一个长度为 m 的序列,第 i 个元素颜色为 bi(保证每个 bi 都是 k 种颜色中的一种,但不保证 k 种颜色都在 b 中出现过)。我们可以修改 b 中若干个位置的颜色,得到一个长度仍为 m 的序列 b′。
我们对 b′ 与 a 中颜色相同的点连这种颜色的一条线段。
如 n=3,m=4,k=3,a={1,2,3},b′={1,3,2,2},它们之间的连线是这样的:
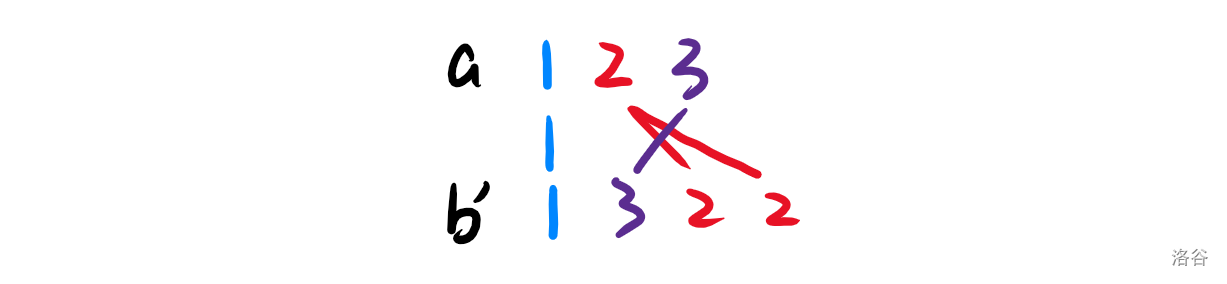
要求不同颜色的线段两两不交,且 k 种颜色都要在 b 中出现,请问最少修改次数是多少?
形式化的,设你修改后的符合要求的序列为 b′,那么你需要最小化:
i=1∑m[bi=bi′]
对于上述 a={1,2,3},b′={1,3,2,2} 的情况,它们之间的连线(红色的 2 与紫色 3 之间)出现了相交。
但如果我们把 b 修改成 {1,2,3,3},它们之间的连线没有相交,满足上述条件:
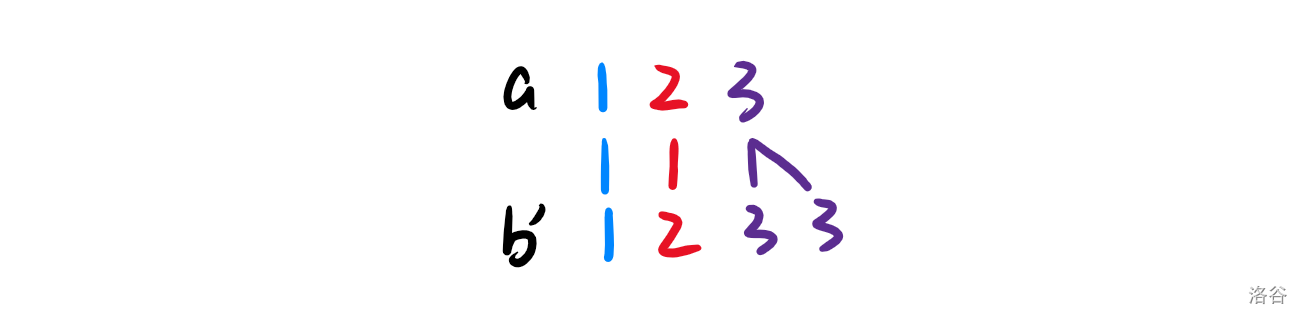
注意:
- b′={1,1,4,5} 的情况连线也没有相交,但是 b′ 包含了 k 种颜色之外的颜色(有 4 和 5),因此这个 b′ 不合法。
- b′={1,1,1,1} 的情况连线也没有相交,但是 b′ 中没有包含 1∼k 中所有的颜色(没有 2 和 3),因此这个 b′ 也不合法。
特别的,如果无论怎样修改都无法满足要求,请输出 -1。
第一行共两个整数 n,m,分别表示序列 a,b 的元素个数。
第二行共 n 个整数,第 i 个整数表示 ai。
第三行共 m 个整数,第 i 个整数表示 bi。
一行,一个整数,表示满足要求的最小修改次数。
如果无论怎样修改都无法满足要求,请输出 -1。
3 4
1 2 3
1 3 2 2
2
5 5
1 2 3 4 4
1 2 3 3 3
1
5 10
1 2 3 4 5
1 2 2 3 2 2 2 4 5 4
3
10 2
1 2 1 2 2 2 2 2 2 2
2 2
-1
Hint
【样例 #1 解释】
将 {1,3,2,2} 修改为 {1,2,2,3}。
可以证明这是修改次数最少的方式。
【样例 #2 解释】
将 {1,2,3,3,3} 修改为 {1,2,3,3,4}。
可以证明这是修改次数最少的方式。
本题开启捆绑测试以及子任务依赖。
本题时限 2s。
| Subtask |
n,m≤ |
分数 |
子任务依赖 |
| 1 |
5 |
无 |
| 2 |
5000 |
35 |
1 |
| 3 |
105 |
30 |
1,2 |
| 4 |
2×106 |
1,2,3 |
- 对于 100% 的数据,保证 1≤n,m≤2×106,1≤ai,bi≤n。设 i=1maxnai=k,保证 1∼k 均在 a 中出现过,且 1≤k≤n。


 京公网安备 11011102002149号
京公网安备 11011102002149号