题目背景

PA 2024 3C

题目描述

题目译自 PA 2024 Runda 3 Obrazy，感谢 Macaronlin 提供翻译

给定尺寸为 $h\times w$ 的矩形墙面，以及 $n$ 种尺寸的正方形画框，每种尺寸画框都有无穷多个。对于任意两种不同尺寸的画框，其中一个尺寸的边长总能整除另一个尺寸的边长。

现用这些画框完全覆盖墙面，而且画框之间不能重叠，只能边缘相接，请求出最少需要购买多少个画框？如果不可能完全覆盖墙面，则程序应输出 $-1$。

输入格式

第一行两个整数 $h$ 和 $w\ (1\le h,w\le 10^9)$，表示墙面大小。

第二行一个整数 $n\ (1\le n\le 30)$，表示画框个数。

第三行 $n$ 个整数 $d_1,d_2,\ldots,d_n\ (1\le d_i\le 10^9,d_i<d_{i+1})$，表示每个正方形画框的大小，保证 $d_{i+1}$ 能被 $d_i$ 整除。

输出格式

输出一行一个整数，如果可以完全覆盖墙面，输出最少要购买多少画框，否则输出 $-1$。

6 10
3
1 3 6

9

3 3
1
2

-1

提示

在第一个样例中，Byteasar 可以用九个画框（六个 $1\times 1$、两个 $3\times 3$ 和一个 $6\times 6$）覆盖一面墙，具体如下：

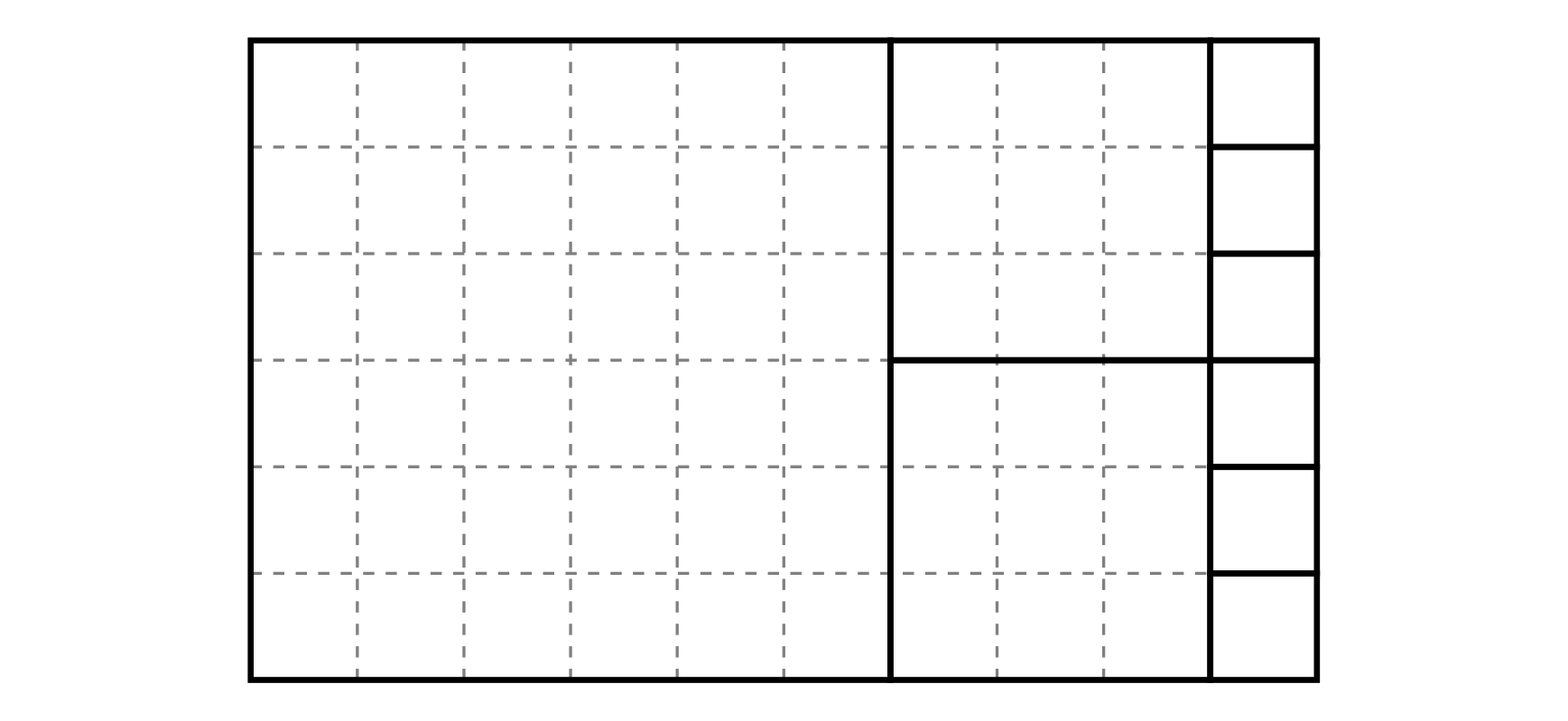
在第二个样例中，无法完全覆盖墙面。