题目描述

Maxwell 有一块巧克力想和他的朋友们分享。巧克力可以看作 $2\times N$ 个小方块组成的，每个小方块的美味度可以表示为 $2 \times N$ 的整数数组 $T_{i,j}$。Maxwell 想把整个巧克力分成若干个连通块，每个连通块的巧克力小方格的平均美味程度都是一样的。Maxwell 想知道根据如上所述，他可以将巧克力棒分成的最大连通块数量是多少。

如果可以通过向上、向下、向左或向右移动的方式访问到每个小方块，则该部分被视为一个连通块。

输入格式

输入的第一行包含一个正整数 $N$ 表示巧克力的长度。

第二行包含 $N$ 个空格隔开的整数，第 $j$ 个整数表示巧克力的第一行第 $j$ 个小方块的美味度 $T_{1,j}$。

类似地，第三行包含 $N$ 个空格隔开的整数，第 $j$ 个整数表示巧克力的第二行第 $j$ 个小方块的美味度 $T_{2,j}$。

输出格式

输出一个整数，表示 Maxwell 最多能把巧克力切分出的连通块数。

2
5 4
6 5

2

5
1 0 1 2 0
0 2 0 3 1

5

提示

【样例 1 解释】

把巧克力分割成 $2$ 块是最优的，一种方案是把右下角的一个小方块作为一个连通块，其余三个小方块作为第二个连通块，如下图所示。

每一个连通块的平均美味度都为 $5$。

【样例 2 解释】

一种获得平均分割巧克力的方案如下图所示：

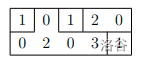
注意每一块的平均美味度都为 $1$。

【数据范围】

本题采用捆绑测试。

对于所有数据，保证 $1 \leq N \leq 2 \times 10^5$，$0 \leq T_{i,j} \leq 10^8$。

下面的表格显示了 $15$ 分的分配方案：